P=Cρv2
La expresión será del tipo:
P=Cρ a vb
donde C es una constante que supondremos adimensional.
Las dimensiones de cada factor son:
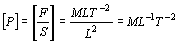
[ ρ ] =ML-3
[ v] =LT-1
Como la ecuación es dimensionalmente homogénea:
P=Cρ a vb ⇒ ML-1T-2=(ML-3)a (LT-1)b ⇒ ML-1T-2=Ma L-3a Lb T–b ⇒ ML-1T-2=Ma L– 3 a + b T–b
Como las bases son iguales los exponentes también lo serán, y tenemos las ecuaciones:
1=a
-1=-3a +b
-2=-b
De la resolución del sistema obtenemos:
a =1; b =2
Luego la ecuación buscada es:
P=Cρ a vb ⇒ P=Cρ v2
P=Cρ v2