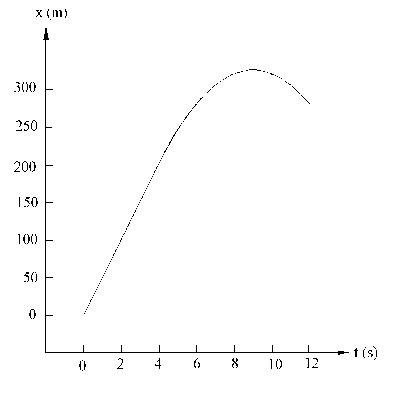v8=10 m/s; v12=-30 m/s; x8=320 m; x12=280 m; xmáx=325 m
En primer lugar hay 4 s en los que no hay aceleración, luego el movimiento es rectilíneo y uniforme. El espacio recorrido será entonces:
x4=vt=50·4=200 m
Después hay aceleración, luego el movimiento es rectilíneo uniformemente acelerado. Para t=8 s tendremos que tener en cuenta que existe espacio inicial (los 200 m que ha recorrido durante los cuatro primeros segundos) , que hay velocidad inicial (los 50 m/s con que se está moviendo la partícula) y que la aceleración es negativa. El tiempo que dura este tipo de movimiento son 4 s. La coordenada x para t=8 s será:
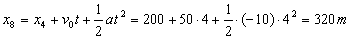
x8=320m
Para t=12 s tendremos que desde t=0 hasta t=4 s el movimiento es como antes, rectilíneo y uniforme, luego se recorren los mismos 200 m que antes. Desde t=4 s hasta t=12 s tenemos ahora 8 s de movimiento rectilíneo uniformemente acelerado. La posición entonces será ahora:
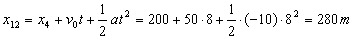
x12=280 m
Ahora vamos a ver la velocidad. Desde t=0 hasta t=4 s el movimiento es rectilíneo y uniforme, luego la velocidad se mantiene constante e igual a 50 m/s:
v4=50 m/s
Desde t=4 s hasta t=8 s transcurren 4 s durante los cuales el movimiento es uniformemente acelerado, luego se alcanzará una velocidad de:
v8=v4+at=50+(-10)·4=10 m/s
v8=10 m/s
Para t=12 s tendremos igual que antes, sólo que el intervalo de movimiento rectilíneo uniformemente acelerado dura 8 s:
v12=v4+at=50+(-10)·8=-30 m/s
v12=-30 m/s
Como la aceleración es negativa la velocidad disminuye con el tiempo. Llegará un momento en que se hará cero y a partir de ahí empezará a ser negativa. Esto implica que el móvil empieza a moverse en sentido contrario volviendo por el mismo camino (disminuiría x). Por ello, la máxima coordenada de x se producirá cuando v=0. Esto sucederá para un tiempo:
v=0 ⇒ vt=v4+at ⇒ 0=50+(-10)t ⇒ t=5 s
La velocidad es nula a los 5 s de llevar movimiento uniformemente acelerado. Como antes de este intervalo había 4 s con movimiento uniforme, el máximo valor de x se alcanzará en t=4+5=9 s. Ahora como antes desde t=0 hasta t=4 se recorren los mismos 200 m, y desde t=4 hasta t=9 tendremos el movimiento uniformemente acelerado luego:
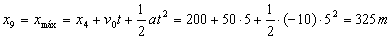
xmáx=325 m
Ahora vamos a construir las gráficas. Empezaremos por la gráfica aceleración-tiempo. Desde t=0 hasta t=4 s no hay aceleración, luego tendremos una recta paralela al eje de tiempos en a=0. Desde t=4 s hasta el final la aceleración es constante y vale -10 m/s2 luego su representación será una recta paralela al eje de tiempos y que pase por el punto a=-10 m/s2. Podemos ver esta gráfica en la figura.

Para la gráfica velocidad-tiempo tendremos que desde t=0 hasta t=4 s el movimiento es rectilíneo y uniforme, es decir, la velocidad es constante. Su representación gráfica será una linea recta paralela al eje de tiempos y que pase por el punto de ordenada v=50 m/s. Desde t=4 s hasta el final el movimiento es rectilíneo uniformemente acelerado. La ecuación que rige este tramo es
v=v4+at=50+(-10)t=50-10t
Es la ecuación de una recta cuya ordenada en el origen es v=50 m/s y cuya pendiente es negativa y vale 10 m/s2. La representación de la velocidad frente al tiempo es la de la siguiente figura.
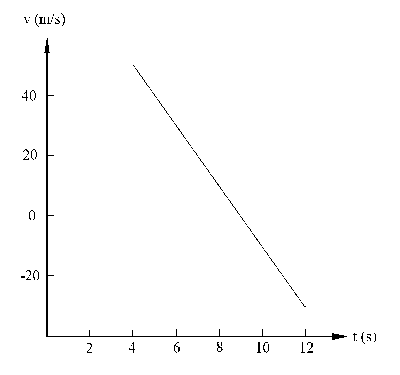
Por último iremos a la gráfica espacio-tiempo. Desde t=0 hasta t=4 s tendremos que por ser el movimiento uniforme la ecuación que liga el espacio con el tiempo, teniendo en cuenta que el espacio inicial es nulo, es:
x=x0+vt=vt=50t
Es la ecuación de una recta que pasa por el origen (0, 0) y cuya pendiente es 50 m/s. Desde t=4 s hasta el final el movimiento es uniformemente acelerado. La ecuación que relaciona en este caso el espacio y el tiempo es:
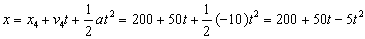
Es la ecuación de una parábola que pasa por los puntos:
|
t (s) |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
x (m) |
245 |
280 |
305 |
320 |
325 |
320 |
305 |
280 |
La representación gráfica del espacio frente al tiempo aparece en esta figura.