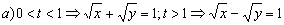
b) Una parábola
c) t=0.5 s
d) (16, 9) y (9, 16)

f) at=2 m/s2; an=2 m/s2
a) Las ecuaciones que tenemos son:
x=t2
y=(t-1)2
De la primera ecuación:
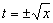
Por tanto tendremos dos casos:

Y de la segunda ecuación:
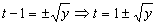
Con lo que también tenemos dos casos:
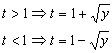
Si agrupamos todas las condiciones e igualamos las t tendremos:
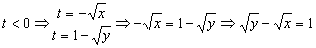
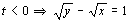
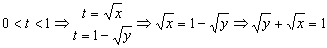
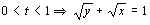
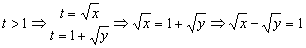
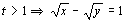
b) Para representar la trayectoria hacemos una tabla de valores para «x» y para «y» y los representamos gráficamente. Tendremos:
|
t |
x |
y |
|
0 |
0 |
1 |
|
1 |
1 |
0 |
|
2 |
4 |
1 |
|
3 |
9 |
4 |
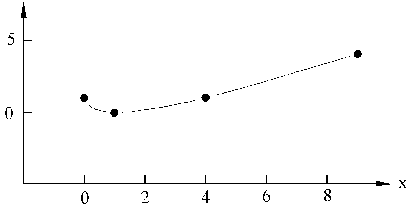
c) La velocidad es la derivada del espacio respecto del tiempo luego tendremos:
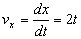
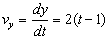
En módulo tendremos que la velocidad es:
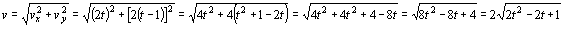
La velocidad será mínima cuando su derivada respecto del tiempo sea nula:
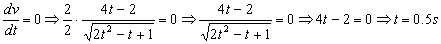
t=0.5 s
d) Si la velocidad es de 10 m/s tendremos:
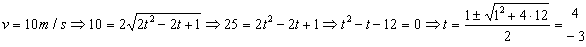
Para t=4 s:
x=t2=42=16 m
y=(t-1)2=(4-1)2=9 m
P=(16, 9) m
Y para t=-3 s:
x=t2=32=9 m
y=(t-1)2=(-3-1)2=16 m
P´=(9, 16) m
e) La aceleración se puede descomponer en sus componentes tangencial y normal:
a=an+at=anun+atut
También podemos calcular sus componentes cartesianas, ya que la aceleración es la derivada de la velocidad respecto del tiempo:
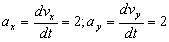
Por tanto:
a=axi+ayj=2i+2j
La velocidad es tangente a la trayectoria luego podemos determinar a partir de la velocidad el vector unitario en dirección tangencial:
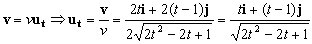
Por tanto:
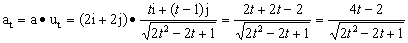
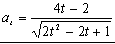
Para calcular la aceleración normal podemos tener en cuenta que en módulo la aceleración es la raíz cuadrada de la suma de sus componentes al cuadrado. Entonces:
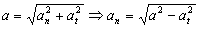
En módulo la aceleración vale:
a2=ax2+ay2=22+22=8 m2/s4
Y la aceleración tangencial al cuadrado:
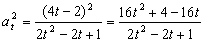
Sustituyendo, la aceleración normal es:
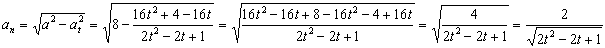
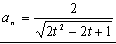
f) Para t=1 s:
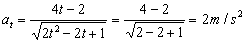
at=2 m/s2
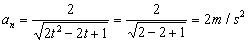
an=2 m/s2