a) L=4 m
b) v=2 m/s
c) v=10.77 m/s
d) θ=68.20^o
e) y_máx=5 m

a) Tendremos una composición de dos movimientos en los ejes X e Y, ambos uniformemente acelerados. En el eje Y la aceleración será la correspondiente a la gravedad, 10 m/s² vertical y hacia abajo. En el eje X sabemos que la fuerza ejercida sobre la pelota es igual a la quinta parte del peso de ésta, luego tendremos que, aplicando la segunda ley de Newton:

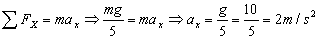
Con esto ya tenemos determinadas las aceleraciones en los dos ejes. En cuanto a velocidades iniciales, la pelota se lanza verticalmente hacia arriba, luego sólo habrá componente de velocidad inicial en la dirección Y:

v_0x=0; v_0y=10 m/s

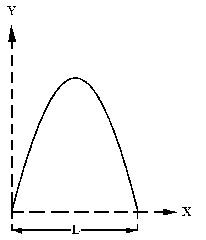
En la figura podemos ver la trayectoria aproximada seguida por la pelota. En el gráfico se ve que para el punto de máximo alcance la altura es nula. Por tanto, para este punto, que llamaremos punto 1, tendremos:

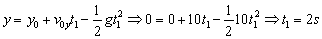
Como la ecuación es de segundo grado se obtienen dos soluciones; la otra solución da t₁=0, que descartamos por corresponder al punto de lanzamiento, en el cual también la altura es nula. Con el valor de t₁=2 s podemos determinar el espacio recorrido en el eje X, que corresponderá con el alcance máximo. Tendremos en cuenta que en el eje X el movimiento también es uniformemente acelerado:

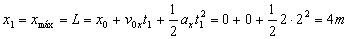
L=4 m

b) Para el punto más alto de la trayectoria (punto que denominaremos 2), la componente vertical de la velocidad se anula luego, la velocidad sólo tiene componente X:

v₂=v_2xi+v_2yj=v_2xi ⇒ v₂=v_2x

Como la componente Y de la velocidad es nula:

v_2y=v_0y-gt₂ ⇒ 0=10-10t₂ ⇒ t₂=1 s

Por tanto la velocidad en el punto 2 será:

v₂=v_2x=v_0x+a_xt₂=0+2·1=2 m/s

v₂=2 m/s

c) En el momento del impacto (punto 1) la velocidad tendrá las dos componentes, que serán:

v_1x=v_0x+a_xt₁=0+2·2=4 m/s

v_1y=v_0y-gt₁=10-10·2=-10 m/s

Vectorialmente tendremos:

v₁=v_1xi+v_1yj=4i-10j

Y en módulo:

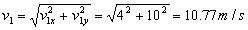
v₁=10.77 m/s

 

d)

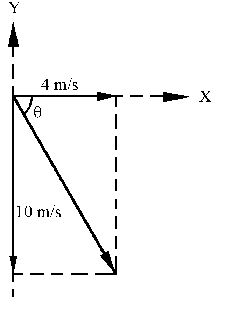
En el punto de impacto si representamos el vector velocidad tendremos lo que aparece en la figura, siendo q el ángulo que forma la velocidad con el suelo. Por trigonometría:

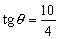
De donde obtenemos:

θ =68.20^º

e) La pelota alcanza su altura máxima en el punto que hemos marcado como 2 luego:

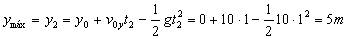
y_máx=5 m