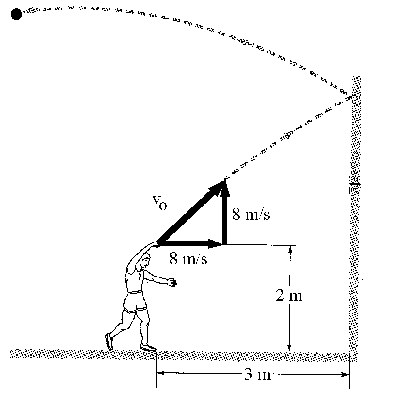
x=11.824 m

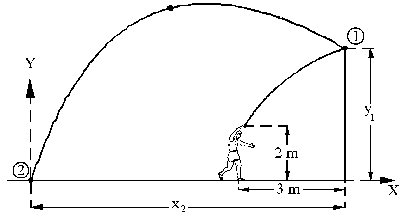
La trayectoria seguida por la pelota es la que aparece en la figura. Desde que la pelota sale de la mano del jugador hasta que llega a la pared en el punto 1, la trayectoria es parabólica. En el eje X la velocidad será constante mientras que en el eje Y el movimiento es uniformemente acelerado, con aceleración la de la gravedad (vertical y hacia abajo). Las velocidades iniciales en los dos ejes en este tramo son:

v_0x=v_x=cte=8 m/s; v_0y=8 m/s

Cuando la pelota alcanza la pared habrá transcurrido un tiempo t₁, que podemos calcular teniendo en cuenta que en el eje X se han recorrido 3 m con velocidad constante:

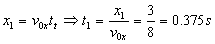
Con ese tiempo determinaremos cuánto vale en ese instante la componente Y de la velocidad:

v_1y=v_0y-gt₁=8-9.8·0.375=4.325 m/s

Y la altura desde el suelo hasta el punto 1 podemos también calcularla:

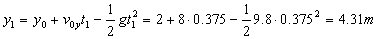
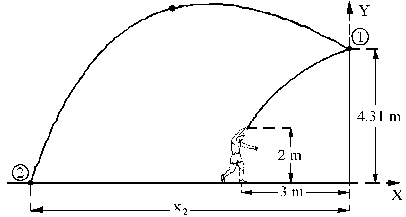
A partir de este punto 1 y hasta el punto 2 tenemos una nueva parábola para la cual tomaremos nuevos ejes. Para esta nueva trayectoria la velocidad inicial es la del punto 1, punto en el cual la componente X cambia de signo, es decir:

v_1x=-8 m/s

Y la componente Y de la velocidad se conserva, luego vale:

v_1y=4.325 m/s

Para el punto de impacto (punto 2) tendré que la altura correspondiente es nula, y llamaré t₂ al tiempo que tarda la pelota en ir desde el punto 1 (origen de esta trayectoria) hasta el punto 2. Teniendo en cuenta que el movimiento en el eje Y sigue siendo uniformemente acelerado:

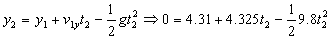
Es una ecuación de segundo grado en t₂, por lo que obtendremos de ella dos soluciones. Una de ellas debe despreciarse por ser negativa, y la otra vale:

t₂=1.478 s

En ese tiempo el valor de x₂ será:

x₂=v_1xt₂=-8·1.478=-11.824 m

El signo es negativo, lo que es lógico si uno se fija en el origen de ejes que hemos tomado; el trayecto desde el punto 1 hasta el 2 se realiza en el sentido negativo de las X. En valor absoluto tendremos:

x₂=11.824 m