a) sí
b) Δh=0.95 m, bajando
a)
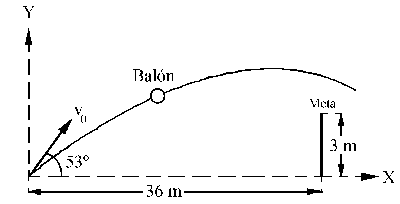
Tendremos un tiro parabólico tal como el que muestra la figura. En el eje X el movimiento es uniforme mientras que en el eje Y el movimiento es uniformemente acelerado con aceleración la de la gravedad (vertical y hacia abajo). Las velocidades iniciales en cada eje son:
v0x=vx=cte=20cos53o=12.036 m/s
v0y=20sen53o=15.973 m/s
En llegar desde el punto de lanzamiento hasta la meta (que llamaremos punto 1) se tarda un tiempo t1 y se recorre un espacio sobre el eje X de 36 m. Entonces:
x1=vxt1 ⇒ 36=12.036t1 ⇒ t1=2.99 s
Para este tiempo la altura a que está el balón será:
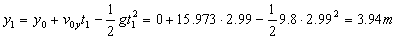
Como la altura de la meta es de 3 m y en ese punto el balón pasa a una altura de 3.94 m, deducimos que sí pasa la barra.
Sí pasa la barra
b) Si la altura del balón es de 3.94 m y la de la barra es de 3 m la distancia entre el balón y la barra será la diferencia:
Δh=y1-hbarra=3.94-3=0.94 m
Δh=0.94 m
Ahora determinaremos el tiempo en que se alcanza la altura máxima. Para el punto de máxima altura (que denominaremos punto 2) la componente en el eje Y de la velocidad es nula. Entonces:
v2y=v0y-gt2 ⇒ 0=15.973-9.8t2 ⇒ t2=1.63 s
De los resultados obtenidos, vemos que el balón pasa sobre la meta en t1=2.99 s mientras que alcanza su altura máxima en t2=1.63 s. Eso quiere decir que primero alcanza la altura máxima y luego pasa sobre la barra de meta, es decir, pasa sobre la barra de meta bajando.
Pasa bajando