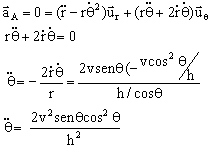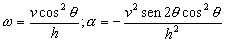
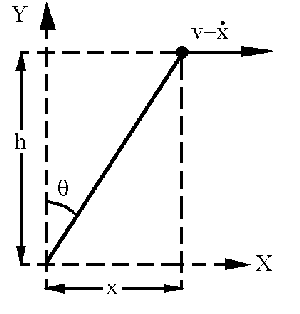
En esquema tendremos lo que muestra la figura. Como el avión sólo se mueve en el eje X, la derivada respecto del tiempo de su posición x será su velocidad v. Como la velocidad del avión es constante su aceleración (segunda derivada de la posición x respecto del tiempo) será nula. Tendremos entonces:
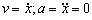
La velocidad angular y la aceleración angular de la visual AO serán respectivamente las derivadas primera y segunda respecto del tiempo del ángulo θ que dicha visual forma con el eje, es decir:
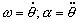
Utilizaremos la expresión trigonométrica de la tangente, ya que en esta expresión aparecen θ, cuya derivada nos interesa porque es la que nos pide el problema, x, cuya derivada es conocida, y h, cuya derivada es nula por ser constante. Entonces:
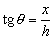
Derivamos esta expresión respecto del tiempo:
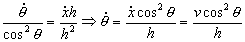
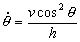Crece en sentido horario
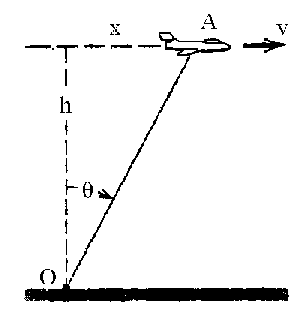
Derivamos ahora otra vez respecto del tiempo:
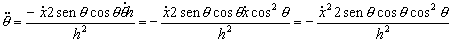
Tenemos en cuenta que:
2senθcosθ=sen2θ
Con lo cual nos queda:
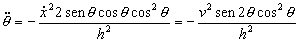
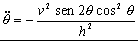
Otra forma de resolver el problema sería:
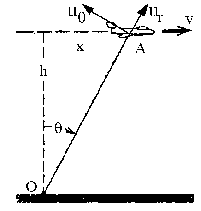
Si expresamos la velocidad en coordenadas polares tendremos:
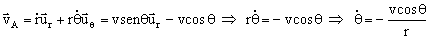
Como:
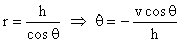
El signo (-) implica que ω es en sentido horario.
Si ahora expresamos la aceleración en coordenadas polares.
