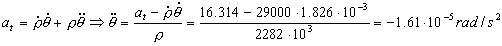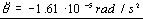ρ=2282 km; α=-1.61·10-5 rad/s2
Ponemos todo en el sistema internacional:
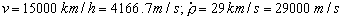
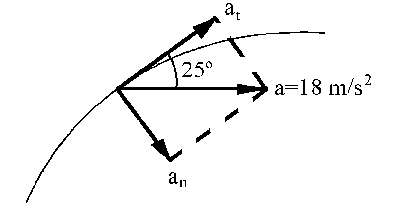
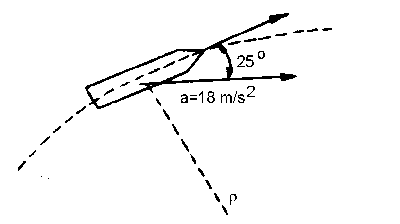
Tendremos las dos componentes de la aceleración que aparecen en la figura. Según el gráfico, y teniendo en cuenta que la dirección normal es la del radio de curvatura y la tangencial la perpendicular, tendremos que la aceleración en componentes intrínsecas vale:
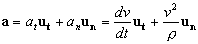
La componente normal podemos ver en el gráfico que vale:
an=18sen25o=7.607 m/s2
Ahora tenemos que la aceleración normal es:
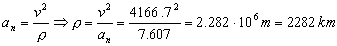
ρ=2282 km
La velocidad en componentes intrínsecas es:
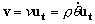
De esta expresión podemos determinar la velocidad de variación del ángulo. En módulo:
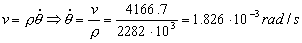
La aceleración tangencial es la derivada del módulo de la velocidad respecto del tiempo:
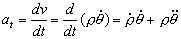
Del gráfico inicial la aceleración tangencial vale:
at=18cos25o=16.314 m/s2
Entonces: