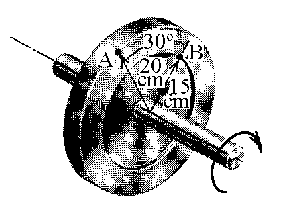vA= 40 cm/s; aB=96.05 cm/s2
Tenemos como datos:
rA=20 cm; rB=15 cm; atA=100 cm/s2; anB=60 cm/s2
Además, por pertenecer los puntos A y B al mismo sólido rígido sus velocidades y aceleraciones angulares son iguales:
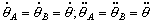
Y como los radios de curvatura son constantes:
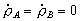
Conocemos la aceleración normal del punto B. Con ella podemos determinar la velocidad de B:
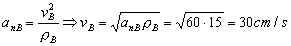
Y la velocidad del punto B en intrínsecas será:
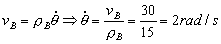
Ahora pasamos al punto A. La velocidad de A será, en intrínsecas:
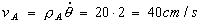
vA=40 cm/s
Para determinar la aceleración angular podemos recurrir a la aceleración tangencial del punto A:
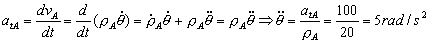
Y por último, para el punto B la aceleración tangencial será:
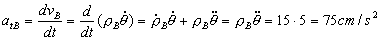
Como las componentes normal y tangencial de la aceleración son perpendiculares, el módulo de la aceleración de B será:
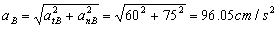
aB=96.05 cm/s2