r=125 cm
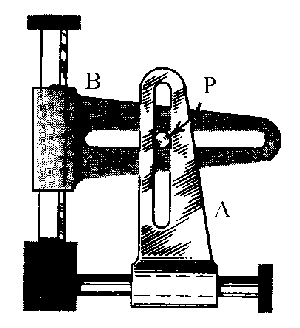
Si dibujamos en coordenadas rectangulares los vectores de los que nos habla el enunciado tendremos lo que aparece en la figura.

En coordenadas cartesianas tendremos por tanto que velocidad y aceleración valdrán, en cm/s y cm/s2 respectivamente:
v=20i-15j; a=-75i+50j
Los módulos de ambos vectores son:
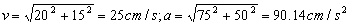
En componentes intrínsecas la velocidad vale:
v=vut
Con esto podemos determinar un vector unitario en dirección tangencial:

Ahora, la aceleración tangencial es la proyección del vector aceleración sobre la dirección tangencial. Para proyectar un vector en una dirección dada se multiplica escalarmente el vector por un unitario en la dirección dada. Según esto:
at=a · ut=(-75i+50j) · (0.8i-0.6j)=-60-30=-90 cm/s2
Y como las aceleraciones tangencial y normal son vectores perpendiculares:
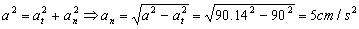
Y con la aceleración normal podemos determinar el radio de curvatura:
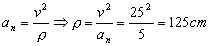
r=125 cm