a) E=3.95·10⁶M J; L=3.65·10¹⁵M kgm²s^-1
b)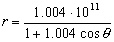
c) r_p=5.01·10¹⁰ m

 

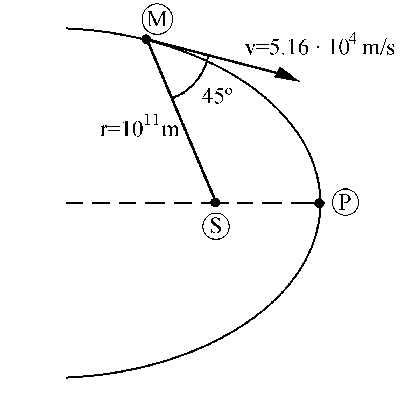
a) Tendremos lo que aparece en la figura. Llamaremos M a la masa del cometa y M_S a la masa del Sol. El momento angular es el producto vectorial del vector de posición por la cantidad de movimiento, luego en módulo será el producto de la cantidad de movimiento por el vector de posición y por el seno del ángulo que ambos vectores forman. Para el punto de la trayectoria que conocemos tendremos:

L=Mrvsenφ=M · 10¹¹ · 5.16 · 10⁴sen45^o=3.65 · 10¹⁵M kgm²/s

L=3.65 · 10¹⁵M kgm²/s

Del mismo modo, como la energía total es constante la podemos calcular en el punto que nos interesa, es decir, donde conocemos velocidad y distancia:

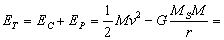
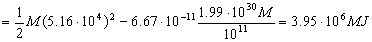
E_T=3.95 · 10⁶M J

Como la energía total es positiva la órbita es una hipérbola.

b) La ecuación general de la cónica es:

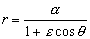
donde r es el radio vector, α la ascensión recta, ε la excentricidad de la cónica y θ el ángulo que forma el radio vector con el origen, tomando como origen el pericentro. La ascensión recta podemos calcularla ya que vale:

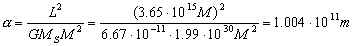
Luego la ecuación de la cónica me queda:

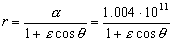
Para determinar la excentricidad necesitaríamos un punto de la cónica en que conociésemos el radio vector y el ángulo θ . Ese punto puede ser el perihelio P. Para este punto tenemos la ventaja de que el radio vector es perpendicular a la velocidad, por lo que el momento angular es directamente el producto del radio por la cantidad de movimiento (el ángulo que forman el radio vector y la velocidad es 90^º y su seno es la unidad). Como tanto la energía como el momento cinético se mantienen constantes, tendremos, que aplicando la conservación de ambos parámetros al punto P obtenemos las ecuaciones:

L=Mr_Pv_P ⇒ 3.65 · 10¹⁵M=Mr_Pv_P ⇒ 3.65 · 10¹⁵=r_Pv_P

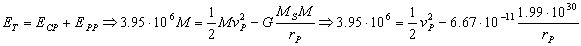
Tenemos un sistema de dos ecuaciones y dos incógnitas, v_P y r_P. De la resolución de este sistema obtenemos:

r_P=5.01 · 10¹⁰ m

Ahora sabemos que cuando r=r_P ⇒ θ=0 ⇒ cosθ=1 y nos queda, sustituyendo en la ecuación de la cónica:

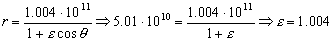
La ecuación de la cónica será entonces:

 

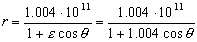
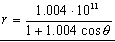
c) La distancia de mayor cercanía al Sol sería la distancia en el perihelio (P) que ya hemos calculado:

r_P=5.01 · 10¹⁰ m