a) M=1.899·1027 kg
b) vmáx=18823 m/s
Conocemos:
rP=350000 km=3.5·108 m; vP=26900 m/s
Llamaremos M a la masa de Júpiter y m a la masa del Voyager I. En el pericentro tenemos la ventaja de que el radio vector es perpendicular a la velocidad, por lo que el momento angular es el producto del radio por la cantidad de movimiento (el ángulo que forman estos dos vectores en ese punto es 90º y su seno la unidad). Como la órbita es parabólica:
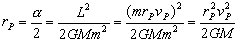
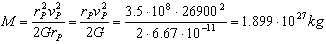
M=1.899 ·1027 kg
b) Del apartado anterior tendríamos la masa de Júpiter:
M=1.899 · 1027 kg
Además conocemos la distancia en el pericentro:
rP=715000 km=7.15·108 m
El momento angular es constante. Eso significa que como es el producto del radio vector por la cantidad de movimiento, cuanto mayor es el radio menor es la cantidad de movimiento y viceversa, de modo que su producto se mantenga siempre constante. Si queremos entonces que la velocidad sea máxima, la distancia será mínima, y esto se produce en el pericentro o punto más próximo al planeta Júpiter. Entonces:
vmáx=vp
Llamaremos m a la masa del Voyager II. En el pericentro tenemos la ventaja de que el radio vector es perpendicular a la velocidad, por lo que el momento angular es el producto del radio por la cantidad de movimiento (el ángulo que forman estos dos vectores en ese punto es 90o y su seno la unidad). Como la órbita es parabólica:
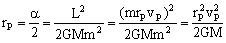
De donde obtenemos:
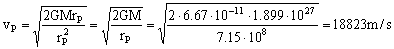
vmáx=18823 m/s