a) dA/dt=2.73·10¹⁰ m²/s
b) v_A=6400 m/s
c) b=7543 km

a) Tendremos lo que aparece en la figura.

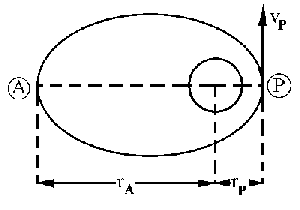
Llamaremos R al radio de la Tierra, M a su masa y m a la masa del Explorer IV. Nos dan las alturas, luego los radios desde el centro de la Tierra son:

r_A=h_A+R=2210+6370=8520 km; r_P=h_P+R=262+6370=6632 km

La velocidad areolar es:

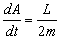
El momento angular es constante, luego podemos calcularle en cualquier punto. Nos interesa el punto P, en el cual conocemos tanto la velocidad como el radio. Además tenemos la ventaja de que tanto en el apogeo como en el perigeo (puntos A y P) el radio vector y la velocidad son perpendiculares, luego el momento angular es el producto del radio por la cantidad de movimiento (no aparece el seno del ángulo que forman estos dos vectores, ya que por ser perpendiculares el ángulo que forman es de 90^º y su seno es la unidad). Tendremos entonces para este punto:

 

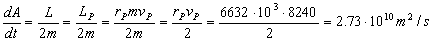
b) El momento angular es constante. Si aplicamos su conservación a los puntos A y P, teniendo en cuenta lo que hemos dicho para ellos en el párrafo anterior, tendremos:

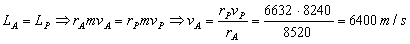
v_A=6400 m/s

 

c) El semieje menor es la media geométrica entre las distancias máxima y mínima, es decir, entre r_A y r_P. Entonces:

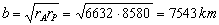
b=7543 km