Problema de Gravitación

Dos estaciones espaciales S1 y S2 recorren en sentido antihorario órbitas coplanarias en torno a la Tierra de radios r0=7000 km y 8r0 respectivamente. 1º) Se desea enviar un vehículo desde S1 hasta S2, y para ello ha de ser lanzado tangencialmente a la órbita de S1 y ha de alcanzar a S2 con una velocidad tangente a la órbita de ésta. Tras un período muy corto de vuelo propulsado, el vehículo irá en vuelo libre de S1 a S2. a) Determinar la velocidad de lanzamiento del vehículo (velocidad relativa a S1). b) Determinar el ángulo θ que define la posición a ocupar por S2 en el momento del lanzamiento. 2º) Inmediatamente después de que S1 lance el vehículo, se pretende hacer regresar a la Tierra dicha estación espacial disminuyendo su velocidad de forma prácticamente instantánea. De esta forma se inicia una trayectoria elíptica de acercamiento a la Tierra, trayectoria cuyo apogeo es el mismo punto en que S1 lanzó el vehículo. Determinar la velocidad de aterrizaje, si el ángulo que define el punto en que aquél se produce es -45o.

1ºa) vrel=2520.4 m/s
1ºb) θ=76o
2º) vat=8083 m/s

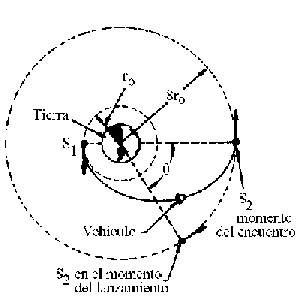
1ºa) Llamaremos M a la masa de la Tierra, mv a la masa del vehículo, mS1 a la masa de la estación S1 y mS2 a la masa de la estación S2. Los radios que conocemos son los de las órbitas de las estaciones S1 y S2, que son:

rS1=r0=7000 km; rS2=8r0=8 · 7000=56000 km

Para determinar la velocidad relativa del vehículo respecto de la estación S1 necesitaremos la velocidad del vehículo y la de la estación en el punto de lanzamiento. Empezaremos por el vehículo. El vehículo sigue una trayectoria elíptica en la cual se conserva la energía total. Si aplicamos la conservación de la energía al punto de lanzamiento, llamando vv a la velocidad del vehículo en este punto tendremos:

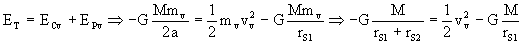
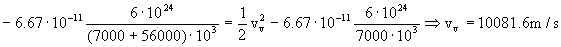
Ahora pasamos a la estación S1. Dicha estación está en una órbita circular. La única fuerza que actúa sobre ella es la de atracción gravitatoria, y la única aceleración que tiene es la normal o centrípeta. Tanto fuerza como aceleración tienen la misma dirección y sentido, luego aplicando la segunda ley de Newton y llamando vS1 a la velocidad de la estación S1 tendremos:

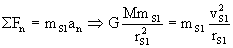
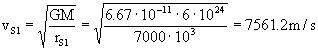
Por tanto la velocidad relativa del vehículo respecto de la estación S1 es:

Vv/S1=vv-vS1=10081.6-7561.2=2520.4 m/s

Vv/S1=2520.4 m/s

 

1ºb) La estación espacial S2 se mueve en una trayectoria circular con velocidad angular constante. Por tanto el ángulo θ podemos determinarlo sabiendo que:

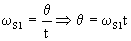
donde t es el tiempo que tarda dicha estación en recorrer el ángulo θ. La velocidad angular es sencilla de calcular si tenemos en cuenta que la estación está en una órbita circular, donde el movimiento es uniforme. En primer lugar, aplicando la segunda ley de Newton y llamando vS2 a la velocidad de la estación S2 tendremos:

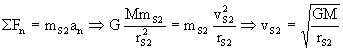
Y como el movimiento es circular uniforme:

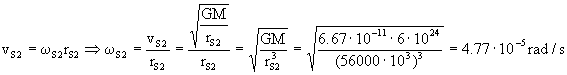
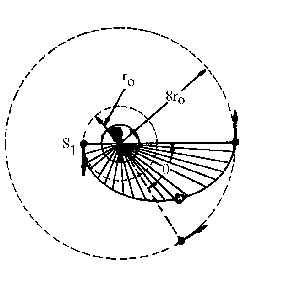Ahora determinaremos el tiempo t. El tiempo t que tarda la estación S2 en recorrer el ángulo θ tiene que ser el mismo que tarda el vehículo en ir desde el punto del lanzamiento hasta el punto del encuentro, ya que salen a la vez y llegan a la vez. Si nos fijamos en el vehículo, éste sigue una trayectoria elíptica. En esta trayectoria la velocidad areolar es constante, es decir, el tiempo empleado en ir desde un punto hasta otro es directamente proporcional al área barrida por el radio vector. Si nos fijamos en el gráfico, desde que el vehículo sale del punto de lanzamiento hasta que llega al punto de encuentro, el radio vector barre la mitad de la superficie S de la elipse (superficie rayada). Teniendo en cuenta que en barrer toda la superficie tardaría el período tendremos:

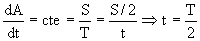
Y el período se puede determinar aplicando la tercera ley de Kepler, que dice que los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores, es decir:

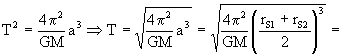
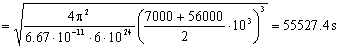
Y el tiempo que buscábamos entonces es:

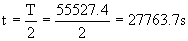
Por tanto el ángulo θ vale:

θ=ωS1t=4.77 · 10-5 · 27763.7=1.32 rad=76º

θ=76º

 

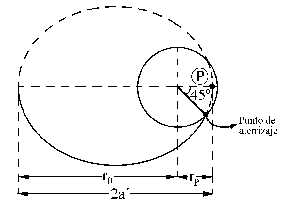2º) Inmediatamente después de que S1 lanza el vehículo se disminuye su velocidad y empieza a recorrer una nueva trayectoria elíptica (que no está dibujada en el enunciado, y cuyos parámetros denotaremos con primas, para distinguirla de la órbita elíptica del vehículo) de acercamiento a la Tierra, de modo que se produce el aterrizaje a un ángulo de -45º, tal como muestra el gráfico que se adjunta. Vamos a determinar la geometría de esta cónica, para luego hallar la velocidad en el punto de aterrizaje por conservación de la energía. La ecuación de esta nueva cónica será:

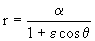
Conocemos dos puntos de la cónica, que son:

Cuando r=r0 ⇒ θ=180º ⇒ cosθ=-1

Cuando r=R ⇒ θ=45º ⇒ cosθ=cos45o

Sustituímos estos dos puntos en la ecuación de la cónica y obtenemos las ecuaciones:

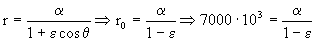
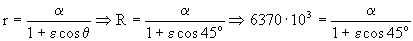
Tenemos dos ecuaciones y dos incógnitas, la ascensión recta (α) y la excentricidad (ε). Resolviendo el sistema obtenemos:

α=6.615 · 106 m; ε=0.055

La ecuación de la cónica es entonces:

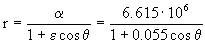
Ahora para el perigeo tendremos:

r=rP ⇒ θ=0o ⇒ cosθ=1

Y nos queda, sustituyendo en la ecuación de la cónica:

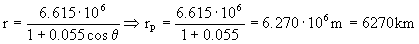
Para la órbita de aterrizaje entonces el eje mayor vale:

2a´=r0+rP=7000+6270=13270 km

En dicha órbita se conserva la energía total. Aplicando la conservación de la energía al punto de aterrizaje:

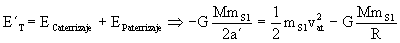
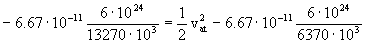
De donde obtenemos:

Vat=8083 m/s