Problema de Gravitación

Dos planetas de masas iguales orbitan alrededor de una estrella de masa mucho mayor. El planeta m1 se mueve en una órbita circular de radio 1·108 km y un período de dos años. El planeta m2 se mueve en una órbita elíptica cuya distancia más próxima es r1=1·108 km y la más alejada r2=1.8·108 km, según se ve en la figura. a) Hallar el período de la órbita de m2; b) ¿Cuál es la masa de la estrella? c) ¿Qué planeta tiene mayor velocidad en el punto P? ¿Cuál tiene mayor energía total? d) ¿Cómo es en comparación la velocidad de m2 en el punto P respecto a la del punto A?

a) T2=3.31 años
b) M=1.49·1029 kg
c) m2
d) vp=1.8 vA

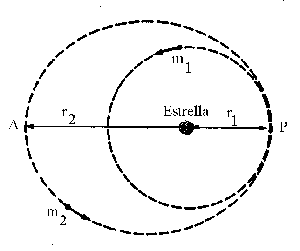
a) Llamaremos M a la masa de la estrella. Los semiejes mayores de las dos órbitas son:

a1=r1=108 km

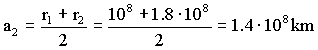
Los períodos se obtendrían aplicando la tercera ley de Kepler, según la cual los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores. Para cada órbita tendremos:

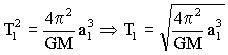
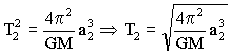
Dividiendo las dos expresiones:

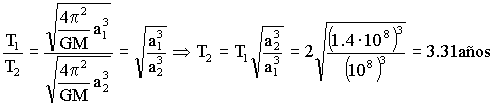
T2=3.31 años

 

b) En uno cualquiera de los períodos, por ejemplo el de m1:

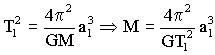
Pasamos el período a segundos:

T1=2 años=2 · 365 · 24 · 3600=6.3072 · 107 s

Sustituyendo:

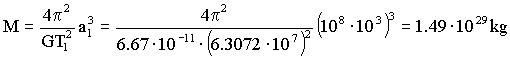
M=1.49 · 1029 kg

 

c) El planeta m1 está situado en una órbita circular, por lo que en ella la velocidad es constante y no depende del punto. La única fuerza a la que está sometido es la de atracción gravitatoria, y la única aceleración que tiene, por ser movimiento circular y uniforme, es la normal o centrípeta. Como fuerza y aceleración tienen la misma dirección y sentido, aplicando la segunda ley de Newton:

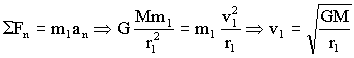
El planeta m2 está situado en una órbita elíptica. En esta órbita se conserva la energía total, por lo que la determinaremos en el punto P, que es donde queremos compararla:

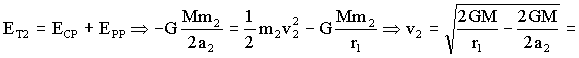
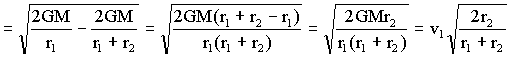
En esta última expresión tenemos que 2r2>r1+r2, lo que implica que en la fracción el numerador es mayor que el denominador, y la fracción es mayor que la unidad. La raíz cuadrada entonces también será mayor que la unidad, lo que implica que:

v2>v1

En cuanto a la energía, para la órbita de m1, que es circular, la energía total vale:

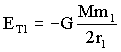
Para la órbita de m2, que es elíptica, la energía total es:

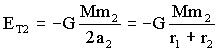
Como las masas de ambos planetas son iguales (m1=m2) el numerador de ambas expresiones es igual. En el denominador es obvio que 2r1<r1+r2, lo que implica que en valor absoluto ET1>ET2; sin embargo, teniendo en cuenta que son negativos:

ET1<ET2

d) En la órbita elíptica de m2 se conserva el momento angular. Además, en los puntos A y P la velocidad es perpendicular al radio vector, por tanto el momento angular en ambos puntos es el producto del radio vector por la cantidad de movimiento (como el ángulo que forman ambos vectores es de 90º su seno es la unidad). Tendremos entonces:

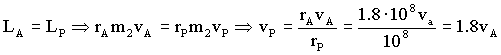
vP=1.8vA