θ=80.97o
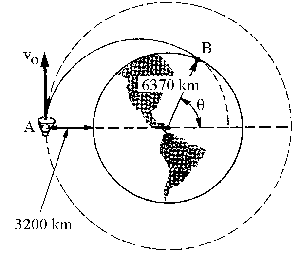
Llamaremos M a la masa de la Tierra, R a su radio y m a la masa de la nave espacial. Conocemos todos los datos de la trayectoria elíptica del aterrizaje en el punto A.
rA=hA+R=3200+6370=9570 km; vA=5400 m/s
Vamos a utilizar la ecuación de la cónica, que es donde aparece el ángulo θ que nos pide el problema. La ecuación que buscamos es:
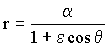
La ascensión recta podemos relacionarla con el momento angular. En el punto A conocemos tanto la velocidad como la distancia. Además, en este punto la velocidad y el radio vector son perpendiculares, luego el momento angular es el producto del radio vector por la cantidad de movimiento (el ángulo que forman estos dos vectores es de 90º y por tanto su seno es la unidad). Tendremos entonces:
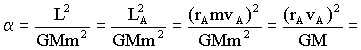
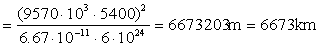
La ecuación de la cónica nos queda:
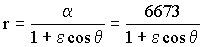
Ahora además conocemos el punto A de la cónica, para el cual r=rA=9570 km y θ=180º, con lo que cosθ=-1. Sustituyendo esto:
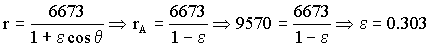
La ecuación de la cónica es, por tanto:
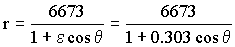
Ahora para el punto de amerizaje tendremos que r=R=6370 km; si aplicamos esto a la cónica:
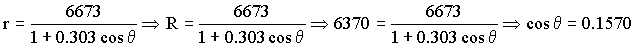
θ=80.97º