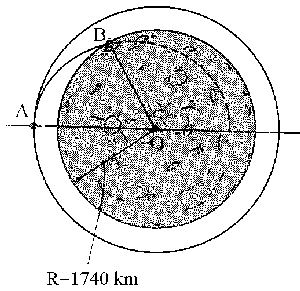
vLEM/M=-153.66 m/s
Llamaremos M a la masa de la Luna, R a su radio, mM a la masa del módulo de comando y mLEM a la del módulo de excursión lunar. La masa de la Luna será:
M=0.0123MT=0.0123 · 6 · 1024=7.38 · 1022 kg
Y conocemos la distancia en el punto A:
rA=hA+R=120+1740=1860 km
Para determinar la velocidad relativa del LEM respecto del módulo de comando necesitaremos ambas velocidades en el punto A, que es donde el LEM es soltado a la deriva. La velocidad del módulo de comando, vM, es sencilla de determinar si consideramos que se encuentra en una trayectoria circular, donde la velocidad es constante. La única fuerza a la que el módulo se halla sometido es la de atracción gravitatoria, y la única aceleración que posee es la normal o centrípeta. Teniendo en cuenta que tanto fuerza como aceleración tienen la misma dirección y sentido, aplicaremos la segunda ley de Newton:
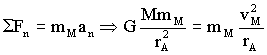
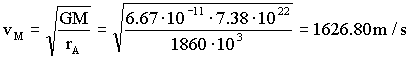
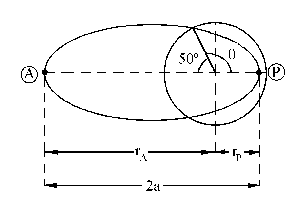 Ahora pasaremos al LEM. El módulo de excursión se encuentra en la órbita elíptica de aterrizaje que aparece en la figura. El aterrizaje se produce a un ángulo:
Ahora pasaremos al LEM. El módulo de excursión se encuentra en la órbita elíptica de aterrizaje que aparece en la figura. El aterrizaje se produce a un ángulo:
θ=180o-50º=130º
Para determinar la velocidad del LEM en el punto A necesitamos determinar el parámetro 2a, para así aplicar la conservación de la energía. Como conocemos la distancia rA vamos a buscar la distancia rP. Para ello utilizaremos la ecuación de la cónica:
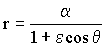
Conocemos el punto A de la cónica, en el cual r=rA ⇒ θ=180o ⇒ cosθ=-1, con lo cual la ecuación de la cónica queda:
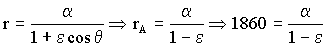
Y conocemos también el punto de aterrizaje, en el que r=R ⇒ θ=130o ⇒ cosθ=-0.643 con lo que tenemos:
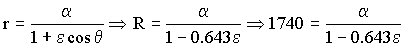
Tenemos entonces dos ecuaciones y dos incógnitas:
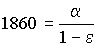
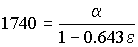
Resolviendo el sistema:
α=1559 km; ε=0.1618
Entonces la ecuación de la cónica es:
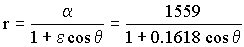
Ahora, para el punto P que es el que nos interesa, cuando r=rP ⇒ θ=0o ⇒ cosθ=1 y tendremos:
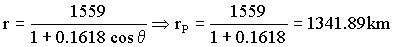
Con esto, el eje mayor de la elipse será:
2a=rA+rP=1860+1341.89=3201.89 km
En esta órbita la energía total se mantiene constante, luego si determinamos la energía en el punto A, llamando vLEM a la velocidad del LEM en este punto tendremos:
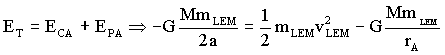

Entonces, la velocidad relativa del LEM respecto del módulo de comando será:
VLEM/M=vLEM-vM=1473.14-1626.80=-153.66 m/s
VLEM/M= -153.66 m/s