Problema de Gravitación

Una estación espacial S se está montando en su órbita circular a 1280 km sobre la Tierra. El cargador de elementos P junto con el cohete portador tiene una masa de 785 kg y se pone en órbita de aproximación en P a 480 km sobre la superficie terrestre. Calcular: a) los períodos de las órbitas (circular y elíptica) correspondientes a la estación S y a la carga P; b) el ángulo θ que describe la posición relativa entre S y P en la puesta en órbita de P de forma que la maniobra de acoplamiento tenga lugar en A según trayectorias paralelas; c) si el cohete portador puede desarrollar un empuje de 890 N, calcular en segundos el tiempo t durante el cual deben encenderse sus motores en las proximidades del punto A para igualar su velocidad a la de la estación S; d) una vez acoplados el cargamento y la estación, ambos realizan una órbita circular completa. Al pasar de nuevo por el punto A se reduce la velocidad del conjunto para iniciar la maniobra de aterrizaje. De este modo se inicia una trayectoria elíptica de aproximación a la Tierra cuyo apogeo es el punto A. Determinar el incremento de velocidad que debe producirse en el punto A para que el aterrizaje tenga lugar a un ángulo de -90o (punto C).

a) TC=6645.59 s; TE=6131.24 s
b) θ=14.01o
c) t=178.48 s
d) ΔvA=-632.82 m/s

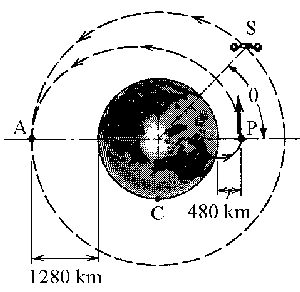
a) Llamaremos M a la masa de la Tierra, R a su radio, mS a la masa de la estación espacial, mC a la masa de la carga y mT a la masa total de la estación y la carga. Tenemos los datos:

rA=hA+R=1280+6370=7650 km

rP=hP+R=480+6370=6850 km

Y el eje mayor de la órbita elíptica es:

2a=rA+rP=7650+6850=14500 km

Los períodos de las dos órbitas se pueden determinar aplicando la tercera ley de Kepler, que dice que los cuadrados de los períodos son directamente proporcionales a los cubos de los semiejes mayores. Según esto, para la órbita circular:

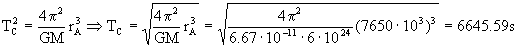
TC=6645.59 s

Y para la órbita elíptica:

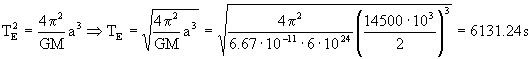
TE=6131.24 s

b) La estación espacial recorre una órbita circular con velocidad angular constante. Si llamamos t al tiempo que tarda dicha estación en ir desde S hasta A, tendremos:

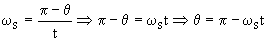
La velocidad angular de la estación es:

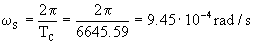
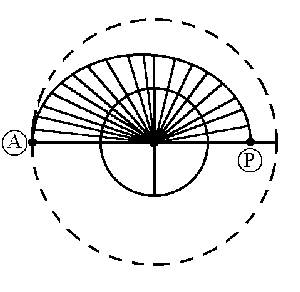Y nos faltaría determinar el tiempo t que tarda la estación en ir desde S hasta A. Como la carga sale a la vez del punto P y llega a la vez al punto A tardará ese mismo tiempo t, luego nos fijaremos en la órbita elíptica recorrida por la carga. Para la órbita elíptica la velocidad areolar es constante, luego el tiempo empleado en ir desde P hasta A será proporcional al área barrida por el radio vector. En el gráfico vemos esta área, que es justo la mitad de la elipse. Teniendo en cuenta lo que hemos dicho, esta área valdrá:

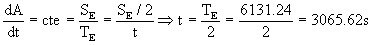
Por tanto, el ángulo θ vale:

θ=π-ωSt=π-9.45·10-4·3065.65=0.245 rad=14.01

θ=14.01º

 

c) En las proximidades del punto A las velocidades son tangentes a la trayectoria, así como la fuerza aplicada por los motores. Por tanto podemos aplicar el teorema del impulso lineal:

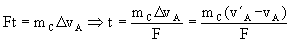
donde v´A y vA son las velocidades de la carga inmediatamente después e inmediatamente antes de la aplicación de la fuerza. Inmediatamente antes de encenderse los motores la carga se encuentra en la órbita elíptica. En esta órbita se conserva la energía, luego:

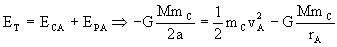
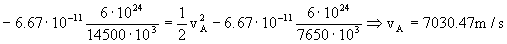
En el punto A e inmediatamente después de la aplicación de la fuerza F la carga se encuentra en la órbita circular de radio rA y su velocidad será v´A. En esta órbita la única fuerza que se ejerce sobre la carga es la de atracción gravitatoria, y la única aceleración que tiene es la normal o centrípeta, dado que en dicha órbita el movimiento es uniforme. Como fuerza y aceleración tienen la misma dirección y sentido, aplicando la segunda ley de Newton:

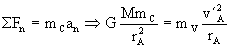
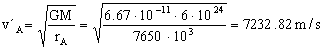
Por tanto, sustituyendo, el tiempo t es:

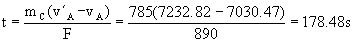
t=178.48 s

 

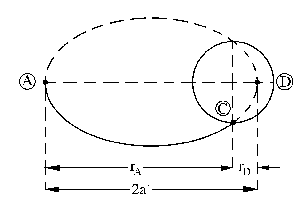d) Una vez acoplados el cargamento y la estación (la masa es ahora la del conjunto mT) éstos inician una nueva órbita elíptica de aterrizaje diferente. Dicha órbita será la que aparece en la figura, con el aterrizaje en el punto C a -90º. El incremento de velocidades en el punto A será la diferencia entre las velocidades del conjunto inmediatamente antes e inmediatamente después del incremento. Inmediatamente antes, a la velocidad del conjunto la llamaremos v´A, ya que es la que tiene el conjunto en la órbita elíptica anterior (órbita PA), es decir:

v´A=7232.82 m/s

En el punto A e inmediatamente después del incremento, el conjunto se encuentra en la órbita elíptica de aterrizaje, cuyo eje mayor será 2a´ (para no confundirle con el de la órbita elíptica anterior), y a la velocidad del conjunto en este punto la denominaremos v´´A. Podríamos determinar la velocidad si conociéramos el parámetro 2a´ de esta trayectoria, para lo cual nos faltaría la distancia mínima que en el dibujo hemos llamado rD. Para calcular todo esto vamos a utilizar la ecuación de la cónica:

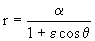
En el punto de aterrizaje (punto C) conocemos r=R ⇒ θ=-90o ⇒ cosθ=0 y nos queda la ecuación:

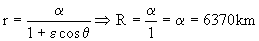
Con esto tendríamos ya una de las constantes de la ecuación determinadas:

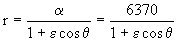
También conocemos los parámetros del punto A, en el cual r=rA ⇒ θ=180o ⇒ cosθ=-1 y tendremos ahora:

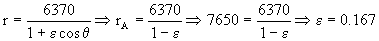
Por tanto la ecuación de la trayectoria es:

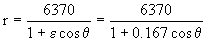
Ahora nos interesaba la distancia en el perigeo. En este punto r=rD ⇒ θ=0o ⇒ cosθ=1 y tendremos:

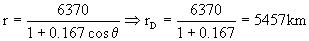
Con esto el eje mayor de la órbita de aterrizaje es:

2a´=rA+rD=7650+5457=13107 km

Por conservación de la energía en el punto A tenemos la ecuación:

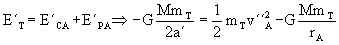
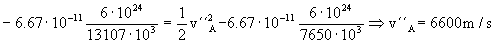
Y la variación de velocidad en el punto A es:

ΔvA=v´´A-v´A=6600-7232.82=-632.82 m/s

ΔvA=-632.82 m/s