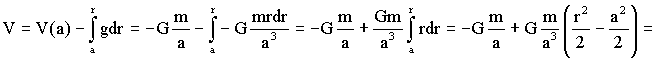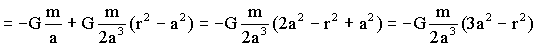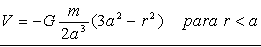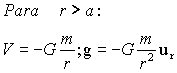
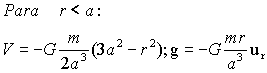
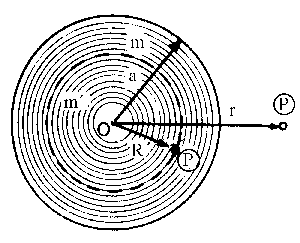
Aprovecharemos en primer lugar lo deducido en el problema de campo y potencial producido por una capa esférica. El campo gravitatorio en el exterior de cualquier distribución de masa con simetría esférica puede considerarse como la superposición de los campos gravitatorios debidos a infinitas cortezas esferas concéntricas y homogéneas (aún cuando puedan tener diferentes densidades), embutidas las unas dentro de las otras como las sucesivas capas de una cebolla. El campo debido a cada una de esas capas, en un punto P exterior a la esfera total, es el mismo que produciría una masa puntual igual a la masa de la capa situada en el centro de la esfera. En consecuencia, el campo total producido en P y el potencial creado son los mismos que los que producirían toda la masa de la esfera supuesta puntual y situada en el centro de la misma, esto es:

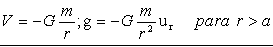
Si el punto P es interior a la esfera (r<a), habrá una serie de capas que están por debajo de él, y otras que están por encima. Respecto a las capas interiores el potencial es:

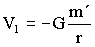
siendo m´ la masa de las capas interiores. Si suponemos que la densidad de la esfera (ρ) es constante por ser una esfera homogénea, la masa m´será:

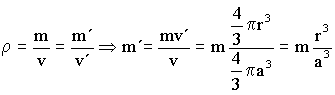
Entonces el potencial V₁ es:

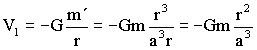
Respecto a las capas exteriores el potencial sería:

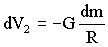
La masa de una esfera diferencial es:

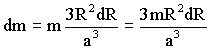
Por lo tanto:

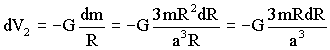
Integrando:

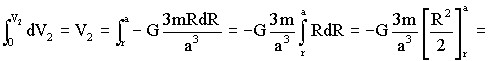
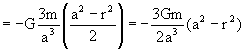
El potencial total será:

 

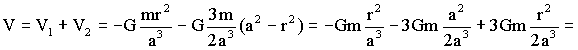
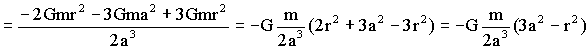
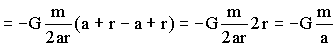
Para el campo derivamos y tendremos:

 

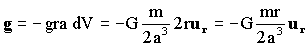
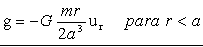
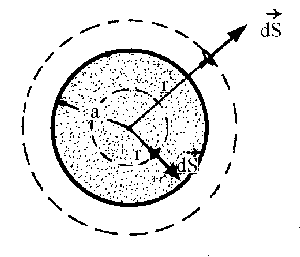Vamos a resolver ahora el mismo problema utilizando el teorema de Gauss. La ley de Gauss dice que el flujo que atraviesa una superficie cerrada arbitraria S es proporcional a la masa que se encuentra en su interior. Dicho flujo vale -4πGm si la masa es interior a la superficie, y es nulo si la masa es exterior a la superficie.

Partiremos en primer lugar de puntos exteriores a la esfera de radio a. Tomamos entonces una superficie gaussiana esférica de radio r>a centrada en el centro de la esfera. Dada la simetría que presenta el problema, el campo gravitatorio en todos los puntos de dicha superficie tendrá la misma magnitud, y será perpendicular a la misma, de modo que:

g · dS=gdS

Tendremos entonces:

 

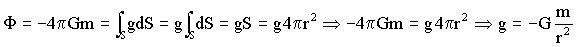
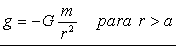
Y para el potencial realizaremos la integración del campo:

 

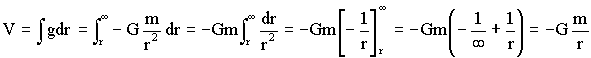
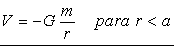
Para puntos interiores a la esfera tomaremos como superficie gaussiana una superficie esférica centrada en el centro de la esfera y de radio r>a. Tendremos ahora:

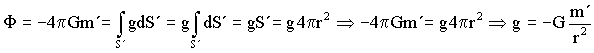
siendo m´ la masa encerrada por debajo del radio r, y que teniendo en cuenta que la densidad de la esfera es constante valdrá:

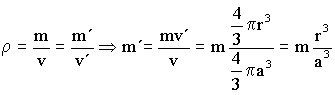
Sustituyendo:

 

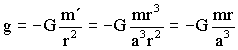
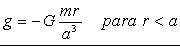
Ahora para el potencial tendremos que integrar: