Tendremos los vectores A y B en la forma:
A=Axi+Ayj+Azk; B=Bxi+Byj+Bzk
El producto escalar de los dos vectores es igual al módulo de un vector, por el módulo del otro por el coseno del ángulo que forman ambos. De esta expresión podemos despejar el coseno:
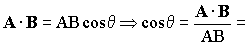
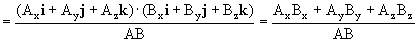
Supongamos ahora que multiplicamos por un escalar c a uno cualquiera de los dos vectores, por ejemplo, al vector A, que me quedaría entonces:
cA= cAxi+cAyj+cAzk
Y teniendo en cuenta lo mismo que antes, tendremos que el coseno del ángulo que forman los vectores cA y B será:
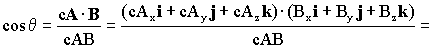
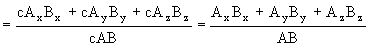
Como puede verse, el coseno del ángulo que forman los vectores no varía, y por tanto no varía el ángulo.