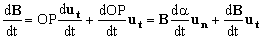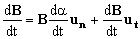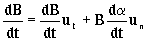
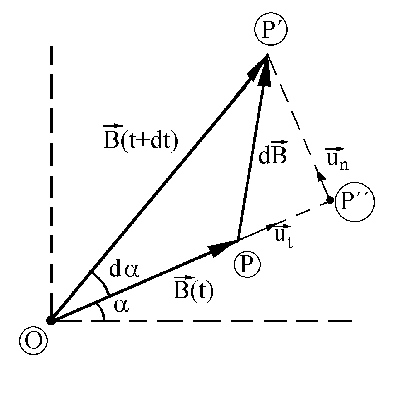
 Tendremos, como aparece en la figura, el vector B(t) (vector OP) función únicamente del escalar t. Cuando el escalar experimenta un incremento dt, el vector experimenta una variación:
Tendremos, como aparece en la figura, el vector B(t) (vector OP) función únicamente del escalar t. Cuando el escalar experimenta un incremento dt, el vector experimenta una variación:
dB=B(t+dt)-B(t)=PP´´+P´´P´
siendo B(t+dt) el vector OP´. Denominaremos ut al vector unitario en la dirección del vector B(t) y un al vector unitario en dirección normal (perpendicular al vector). Podemos descomponer dB en estas dos componentes, y tendremos:
dB=P´´P´un+PP´´ut
El vector P´´P´ será:
P´´P´=Bdα
Y el vector PP´´ es la variación del módulo de B:
PP´´=dB
Tendremos entonces:
dB=Bdα
un+dBut
Y dividiendo por dt tendremos la solución:
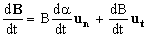
Tenemos otra forma de hacerlo. La componente tangencial de la derivada de un vector, indica la variación del módulo del vector, mientras que la componente normal indica la variación de la dirección del vector. Teniendo en cuenta esto, tendremos que el vector B(t) es:
B(t)=But=OPut
OP será el módulo del vector y ut un vector unitario en la dirección del vector. Ambas cantidades don variables. Si derivamos respecto de t tendremos:
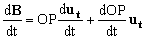
Como ut es un vector de módulo constante su módulo será:
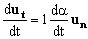
donde un es un vector normal (perpendicular) a ut. Por tanto, sustituyendo en la expresión de la derivada de B y teniendo en cuenta que OP es el módulo del vector: