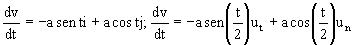
Las componentes cartesianas de la derivada de la velocidad son sencillas de determinar, ya que no habría más que derivar este vector:

 

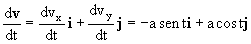
Las componentes intrínsecas son la normal y la tangencial. Llamaremos u_n a un vector unitario en la dirección normal, y u_t a un vector unitario en la dirección tangencial. Estos dos vectores son perpendiculares. Hemos obtenido del problema anterior:

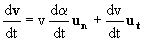
El módulo del vector v es:

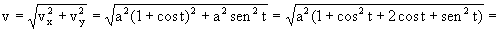
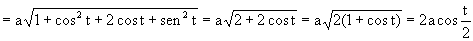
Por tanto la derivada del módulo de la velocidad es:

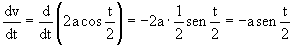
Ahora nos falta determinar la derivada de a
respecto del tiempo. Para ello vamos a representar el vector velocidad. Su componente en el eje X es:

v_x=a(1+cost)=a+acost

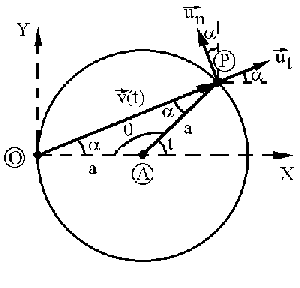Tendríamos, en una circunferencia de radio a, el vector v con su origen en el borde de la circunferencia, tal como se muestra en la figura, de modo que puede verse que si t es el ángulo marcado, la componente en X del vector v es la dada por el problema. Además, la componente Y de este vector es:

v_y=asent

Además, el triángulo OAP es isósceles (dos de sus lados valen a) lo que implica que dos de sus ángulos son iguales (los ángulos α). En el triángulo OAP se cumplirá que:

2α+θ=180^º

Y además podemos ver que:

θ+t=180^º

Como los segundos miembros son iguales, los primeros también lo serán luego:

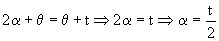
Si diferenciamos:

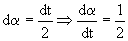
Entonces tendremos:

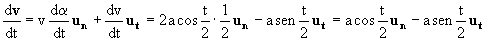
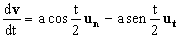
Vamos a comprobar ahora que ambas soluciones son idénticas. Para ello vamos a expresar los vectores unitarios u_t y u_n en función de i y j:

Sustituyendo en la expresión de la derivada de la velocidad nos queda:

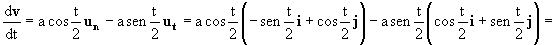
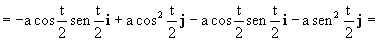
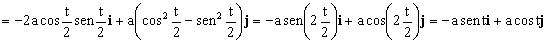
Podemos ver que es la misma expresión que hemos obtenido en coordenadas cartesianas.

Ahora tenemos que determinar los valores de t para los cuales se verifica que 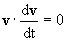. Tendremos, si utilizamos las componentes cartesianas:

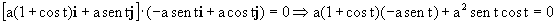
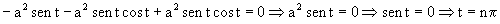
donde n tomaría valores enteros desde cero en adelante:

t=nπ, con n=0, 1, 2,…

Esta expresión es general, es decir, nos dice cuándo es nulo el producto escalar, o bien porque sea nulo el vector v, o bien porque sea nula su derivada, o bien porque sean dos vectores perpendiculares, en cuyo caso el ángulo que forman es de 90^º, cuyo coseno es cero (véase la definición de producto escalar). Vamos a ver cuándo es nulo el producto escalar siendo ambos vectores distintos de cero. Para que el producto escalar sea nulo acabamos de ver que los dos vectores deben ser perpendiculares. Los dos vectores son, en componentes intrínsecas:

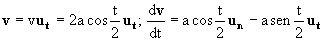
Podemos ver que el vector v sólo tiene componente tangencial, por lo que para que el vector derivada sea perpendicular a él, dicho vector sólo puede tener componente normal. Esto implica que la componente tangencial del vector derivada debe ser nula:

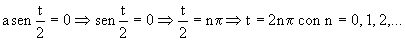
Esto quiere decir que el producto escalar es nulo cuando t es un número entero de veces p
, correspondiendo los números pares a casos en que ese producto es nulo porque los dos vectores son perpendiculares, y los números impares a casos en que el producto es nulo porque uno cualquiera de los dos vectores es nulo.
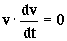