a)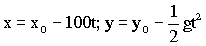
b)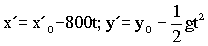
c) θ=± 29^o

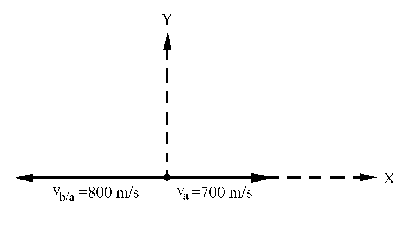a) La Tierra se puede suponer fija, luego todas las velocidades, posiciones y aceleraciones que estén medidas respecto de la Tierra serán las absolutas. Tenemos que el proyectil es lanzado hacia atrás con una velocidad de 800 m/s respecto del avión, mientras que el avión avanza hacia delante a una velocidad de 700 m/s. Llamaremos v_a a la velocidad absoluta del avión, y v_b/a a la velocidad de la bala respecto del avión. Además, tomaremos el eje X en la dirección de avance del avión, y el eje Y en dirección perpendicular, y positivo hacia arriba, tal como aparece en el gráfico adjunto. Buscamos en primer lugar las ecuaciones del movimiento absoluto de la bala, luego su velocidad inicial será:

v_b/a=v_b–v_a ⇒ v_b=v_b/a+v_a=-800i+700i=-100i

En el eje X no hay ninguna aceleración, luego el movimiento es uniforme y la ecuación que define la posición en el eje X es:

x=x₀+v_bt=x₀-100t

x= x₀-100t

En el eje vertical la bala está sometida a la aceleración de la gravedad, que será vertical y hacia abajo. Además, en este eje no tendríamos velocidad inicial, ya que la velocidad inicial de la bala sólo tiene componente en el eje X:

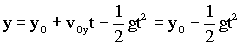
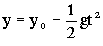
b) Si tomamos un sistema de referencia en el avión, la velocidad inicial de la bala respecto del avión será:

v_b/a=-800i

En este eje seguiremos teniendo movimiento rectilíneo y uniforme, luego la posición respecto del avión en cada instante, que llamaremos x´ es:

x´=x´₀+v_b/at=x´₀-800t

x´= x´₀-800t

Y en el eje Y tendremos igual que antes que la bala respecto del avión está sometida a una aceleración que es la de la gravedad, vertical y hacia abajo, y que la velocidad inicial en este eje es nula luego:

 

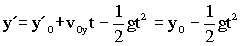
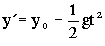
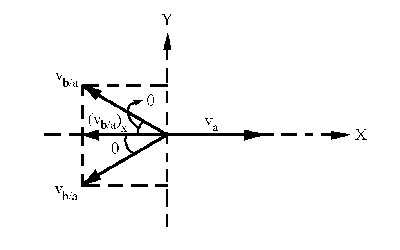c) Ahora tenemos que la bala se lanza con un cierto ángulo θ, de modo que la componente horizontal de la velocidad es nula. Como puede verse en el dibujo este ángulo puede ser positivo o negativo, de modo que en ambos casos la componente horizontal de la velocidad relativa puede anularse con la velocidad absoluta del avión. Si nos fijamos únicamente en el eje X tendremos que:

(v_b/a)_x=(v_b)_x-(v_a)_x ⇒ (v_b)_x=(v_b/a)_x+(v_a)_x

0=-800cosθ+700

De donde obtenemos:

θ=±29^º