a_rel=2.688 m/s²

En primer lugar pasaremos la velocidad al Sistema Internacional:

v_A=v_B=48.3 km/h=13.42 m/s

El coche B es un sistema de referencia en rotación, por lo que la aceleración de A en función de B es:

a_A=a_B+α X BA-ω²BA+2ω X v_r+a_r ⇒ a_r= a_A–a_B-α X BA+ω²BA-2ω X v_r

Vamos a ir determinando cada uno de los términos que aparecen en la ecuación. El coche A lleva movimiento rectilíneo y uniforme, luego:

a_A=0

El coche B se mueve en un arco de circunferencia con velocidad constante. De las dos componentes de aceleración que podría tener, tangencial y normal, la tangencial es nula, ya que el módulo de la velocidad es constante. La única componente de la aceleración será la normal, que valdrá:

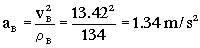
Tomaremos un sistema de ejes coordenados, con el eje X horizontal y hacia la derecha, el eje Y vertical y hacia arriba, y el eje Z perpendicular a ambos y hacia fuera. Según estos ejes, la aceleración de B por ser normal tiene la dirección del radio de curvatura y apuntando hacia el centro, es decir:

a_B=1.34j

El vector de posición es:

BA=134j

El coche B se mueve con velocidad angular constante, luego la aceleración angular será nula:

α=0 ⇒ α X BA=0

La velocidad angular, teniendo en cuenta la velocidad lineal del coche B, vale:

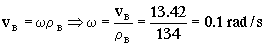
Vectorialmente:

ω=0.1k

Por último, para determinar la velocidad relativa expresamos la velocidad del coche A en función del B, y tendremos:

v_A=v_B+ω X BA+v_r ⇒ v_r=v_A–v_B-ω X BA

Con el sistema de ejes tomados las velocidades de los coches son:

v_A=-13.42i: v_B=13.42i

Sustituyendo:

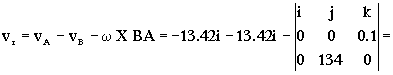
=-13.42i-13.42i-13.4i=-13.44i

 

Sustituyendo en la aceleración relativa:

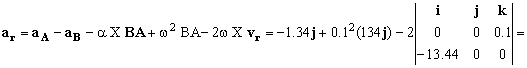
=-1.34j+1.34j+2.688j=2.688j

En módulo:

a_r=2.688 m/s²