a) aA=632j cm/s2
b) aA=-916j cm/s2
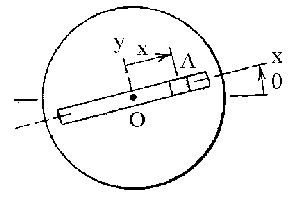
a) Vamos a ver qué ocurre primero cuando x=0. Tomaremos como sistema de referencia los ejes XY marcados en la figura original, y un eje Z perpendicular a los mismos y con sentido positivo hacia fuera. La aceleración del punto A será:
aA=aO+αXOA-ω2OA+2ω X vr+ar
En primer lugar el punto O es un punto fijo que no tiene ni velocidad ni aceleración, luego:
aO=0
Para la velocidad angular tendremos:

Cuando x=0 tendremos:
x=0 ⇒ 5sen(4πt)=0 ⇒ sen(4πt)=0 ⇒ 4πt=0 ⇒ t=0
Para t=0 entonces la velocidad angular es:
ω=1.6πcos(8πt)=1.6πcos0=5.03 rad/s ⇒ ω=5.03k
La aceleración angular:

Cuando t=0:
α=-0.2(8π)2sen(8πt)=-0.2(8π)2sen0=0
La velocidad relativa es la que tiene la corredera en el sistema de referencia en movimiento. En dicho sistema la corredera únicamente puede moverse a lo largo de la ranura, luego la velocidad relativa y la aceleración relativa tienen la dirección de la ranura, es decir, del eje X. La velocidad relativa es:

Para t=0:
vr=5 · 4πcos(4πt)= 5 · 4πcos0=62.83 cm/s ⇒ vr=62.83i
Y la aceleración relativa:
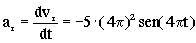
Y para t=0:
ar=-5 · (4π)2sen(4πt)=-5 · (4π)2sen0=0
Sustituyendo todo tenemos:

aA=632j cm/s2
b) Ahora, cuando x=5 cm:
5=5sen(4πt) ⇒ sen(4πt)=1 ⇒ 4πt=π/2 ⇒ t=0.125 s
Por tanto ahora tendremos como antes que el punto O sigue siendo un punto fijo:
aO=0
El vector de posición es:
OA=xi=5i
La velocidad angular:
ω=1.6πcos(8πt)=1.6πcos(8π· 0.125)=-5.03 rad/s ⇒ ω=-5.03k
La aceleración angular:
α=-0.2(8π)2sen(8πt)=-0.2(8π)2sen(8 · 0.125π)=0
La velocidad relativa:
vr=5 · 4πcos(4πt)= 5 · 4πcos(4π· 0.125)=0
Y la aceleración relativa:
ar=-5 · (4π)2sen(4πt)=-5 · (4π)2sen(4π· 0.125)=-789.57 cm/s2 ⇒ ar=-789.57i
Entonces sustituyendo:
aA=aO+αXOA-ω2OA+2ω X vr+ar=-ω2OA+ar=-5.032(5i)-789.57i=-916i cm/s2
aA=-916icm/s2