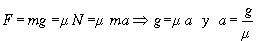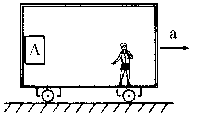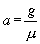
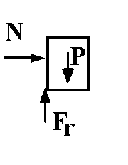
Aislamos el bloque A y hacemos el diagrama de sólido libre:
Aplicamos la segunda ley de Newton: ΣF=ma
En las direcciones X e Y tendremos, respectivamente:
N=m a
Fr-P=0 como P=m g ⇒ Fr=m g
Donde N es la componente normal de la acción de la pared del vagón sobre el bloque A, Fr es la componente tangencial de dicha acción ó fuerza de rozamiento, «m» es la masa del bloque, «a» su aceleración, P el peso y «g» la aceleración de la gravedad.
Por otra parte la fuerza de rozamiento es máxima por lo que:
Fr= μN
Teniendo en cuenta además las dos ecuaciones anteriores, determinamos el valor de la aceleración del bloque A.
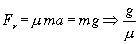
Podemos relacionar las aceleraciones del bloque a y del vagón av por la expresión:
a=av+ ab/v
Siendo ab/v la aceleración relativa del bloque respecto al vagón, que en este caso es nula, al no existir movimiento relativo del bloque respecto al vagón. Podemos por tanto concluir que las aceleraciones del vagón y el bloque son iguales.
Para el observador situado en el vagón el bloque estaría en equilibrio, puesto que él solo apreciaría el movimiento relativo del bloque respecto al vagón. ¿Cómo aplicaríamos en este caso las leyes de Newton? Considerando que además de las fuerzas reales actúan sobre el bloque las fuerzas de inercia; aquí: Fi = – m av
El diagrama de sólido libre será:
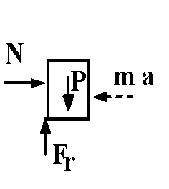
N-m a=0
Fr-P=0
