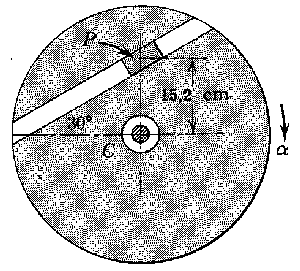
Problema de Dinámica de la Partícula

El disco ranurado gira en un plano horizontal en torno a su árbol que pasa por C, mientras que la corredera P de 450 g puede moverse libremente en la guía lisa. Partiendo del reposo con la corredera en la posición indicada, se proporciona al disco una aceleración angular en el sentido de las agujas del reloj de 40 rad/s2. Calcular la fuerza en el plano horizontal F ejercida por la guía sobre P al iniciarse el movimiento y la aceleración inicial de P relativa a la ranura.

F=1.37 N; ar=5.28 m/s2

Como el disco gira en un plano horizontal el peso de la corredera se equilibra con la reacción normal, ambos en la dirección perpendicular al movimiento. Por otra parte, como la guía y la corredera son lisas, no hay que considerar fuerzas de rozamiento. Tomaremos como sistema de referencia el eje X coincidente con la dirección de la ranura en ese instante y el eje Y perpendicular a ella.

La aceleración de la corredera es:

a=aC+α X CP+ω X (ω X CP )+2(ω X vr)+ar

Como C es un punto fijo aC=0. Además, al iniciarse el movimiento ω y vr también serán vectores nulos. La aceleración absoluta de la corredera quedará reducida a:

a=α X CP+ar

La aceleración relativa a la ranura ar tendrá la dirección de la misma, es decir, únicamente tendrá componente sobre la dirección X, mientras que tendremos que proyectar en estos ejes el vector de posición CP en ese instante. Tendremos entonces:

a =-a k=-40k

CP=0.152sen30oi+0.152cos30oj=0.076i+0.132j

ar=-ari

El sentido de la aceleración relativa lo suponemos arbitrariamente. Sustituyendo todo, la aceleración de la corredera será:

a=α X CP+ar=(-40k) X (0.076i+0.132j)-ari=(5.28-ar)i-3.04j

Si ahora hacemos el diagrama del sólido libre tendremos:

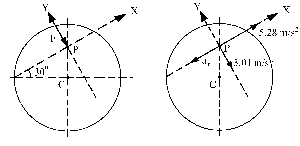
Aplicamos la segunda ley de Newton teniendo en cuenta los ejes de la figura:

Σ FX=maX ⇒ 0=m(5.28-ar) ⇒ 5.28-ar=0

ar=5.28 m/s2

Como sale positivo, el sentido supuesto era correcto.

Σ Fy=maY ⇒ -F=-3.04m ⇒ F=3.04m=3.04 × 0.450=1.37 N

F=1.37 N