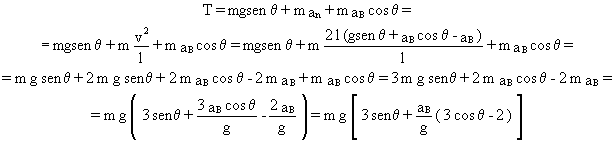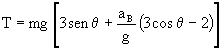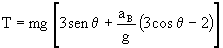
Para un observador inercial tenemos:

Σ F=ma

Tomamos unos ejes de coordenadas X y Y tales que X tenga la dirección del hilo e Y perpendicular a dicha dirección, en el plano del movimiento. En cuanto al sistema de fuerzas actuarán la tensión del hilo y el peso del péndulo, mientras que la aceleración absoluta del péndulo estará formada por la suma de la aceleración del punto B más la aceleración relativa. A su vez, la aceleración relativa tendrá dos componentes, la normal en la dirección del hilo (radio de curvatura) y apuntando hacia B (centro de curvatura) y la tangencial. Haciendo el diagrama del sólido libre:

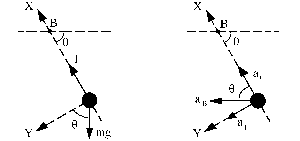
Aplicamos la segunda ley de Newton en cada uno de los ejes:

Σ F_X=ma_X ⇒ T-mgsenθ =ma_n+ma_Bcosθ ⇒ T=mgsenθ +ma_n+ma_Bcosθ

Teniendo en cuenta que la aceleración normal vale:

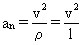
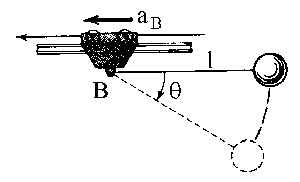
Tendremos que la expresión para la tensión del hilo es:

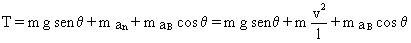
Para determinar la tensión T del hilo hemos de determinar el valor de v. Dicho valor podemos obtenerlo de la ecuación correspondiente al otro eje:

Σ F_Y=ma_Y ⇒ mgcosθ =ma_t+ma_Bsenθ ⇒ a_t=gcosθ -a_Bsenθ

El valor de la aceleración tangencial es:

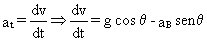
Multiplicamos y dividimos en el primer miembro por un arco diferencial ds:

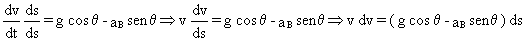
Teniendo en cuenta que el arco diferencial vale ds=ldθ la ecuación nos quedará:

vdv=(gcosθ -a_Bsenθ )ldθ

Integramos teniendo en cuenta que el sistema parte del reposo, es decir, que cuando θ =0 ⇒ v=0, tendremos:

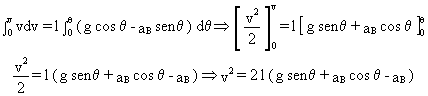
Sustituyendo este valor en la expresión de la tensión nos queda: