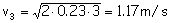Problema de Dinámica de la Partícula

Los sistemas representados en la figura están inicialmente en reposo. Despreciando las masas de las poleas y el rozamiento en sus ejes, determinar para cada sistema: a) la aceleración del bloque A; b) la velocidad de dicho bloque transcurridos 4 s; c) la velocidad del mismo cuando ha recorrido 3 m.

a) a1=3.27 m/s2; a2=4.89 m/s2; a3=0.23 m/s2
b) v1=13.08 m/s; v2=19.56 m/s; v3=0.92 m/s
c) v1=4.43 m/s; v2=5.42 m/s; v3=1.17 m/s

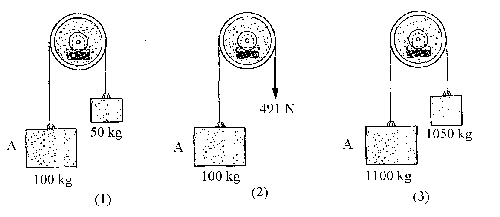
a)Trazamos los diagramas de sólido libre para los bloques y las poleas en los tres casos, y aplicamos la segunda ley de Newton a los bloque y poleas

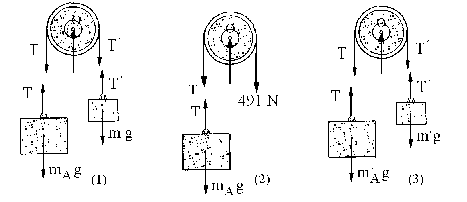
En el caso (1) tenemos:

ΣM0=I0α ⇒ T´r-Tr=(1/2) mP r2α =0 (puesto que la masa de la polea, mP, es despreciable) ⇒ T=T´

mA g -T= mA a1

T´-mg= ma1, como T=T´·T-mg= ma1

Resolviendo el sistema de ecuaciones nos queda:

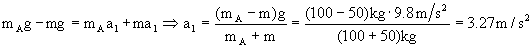
En el caso (2)

Tr-491r=(1/2) mP r2α=0 (puesto que la masa de la polea, mP, es despreciable) ⇒ T=491 N

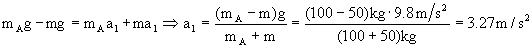
En el caso (3), semejante al (1)

Tr-T´r=(1/2)·mPr2α=0 (puesto que en este caso también la masa de la polea, mP, es despreciable) ⇒ T=T´

mAg -T= mAa3

T´-mg= ma3, como T=T´·T-mg= ma3

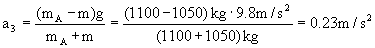
b) Como las fuerzas que actúan sobre el bloque A, en todos los casos, son constantes el movimiento del mismo es uniformemente acelerado. Podemos aplicar, para determinar su velocidad, las ecuaciones de dicho movimiento:

vf=vi+at y sf=si+vit+(1/2) a t2 , como inicialmente están en reposo vi=0

Caso(1)

vf=v1= a1t= 3.27 m/s2 4 s=13.08 m/s

Para el caso (2)

vf=v2= a2t= 4.89 m/s2 4 s=19.56 m/s

En el caso (3)

vf=v3=a3t= 0.23 m/s2 4 s=0.92 m/s

Podríamos haber resuelto este apartado b aplicando el teorema del impulso: F dt=mAdv

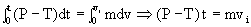
c) Podemos aplicar nuevamente las ecuaciones del movimiento uniformemente acelerado, ahora 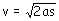o bien aplicar el teorema de las fuerzas vivas en cuyo caso tendremos:

F·ds=ΔEC

(1)

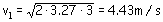
(2)

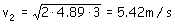
(3)