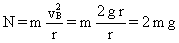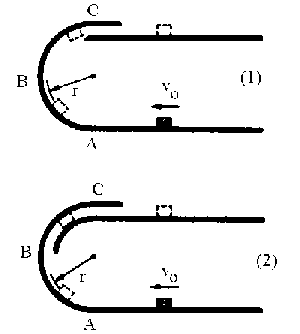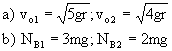
BUCLE 1:
a) Desde el punto de vista de las fuerzas, el paquete se depositará en C siempre que no se anule antes la fuerza normal ejercida sobre el mismo por la pared del bucle, pues si esto sucediera el paquete no seguiría más la trayectoria circular y caería bajo la acción de su peso. Si la normal se anula justo en C, el paquete caería ya sobre la horizontal.
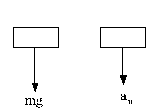
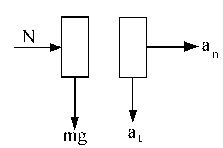
Hacemos el diagrama del sólido libre del paquete en C, teniendo en cuenta que justo ahí se anula la normal. En ese punto:
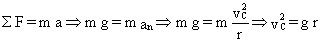
Como no hay rozamiento se conserva la energía entre A y C. Tomamos el nivel de A como nivel de energía potencial nula. En A, por tanto, sólo habrá energía cinética, y en C tendremos energía potencial y cinética:
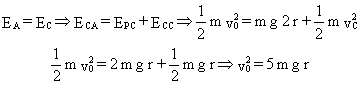
De donde:
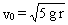
b) Para determinar la normal en B hacemos el diagrama del sólido libre en ese punto y tendremos:
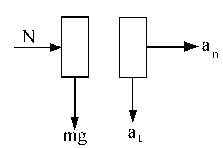
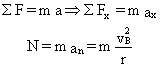
La velocidad vB la determinamos aplicando el principio de conservación de la energía entre los puntos A y B. En A, como antes, sólo habrá energía cinética, mientras que en B tendríamos energía cinética y potencial:
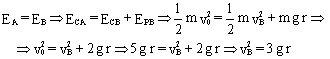
Sustituyendo en el valor de la normal tenemos:
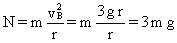
BUCLE 2:
a) En este otro caso la normal puede anularse antes de llegar a C, pues el paquete caería sobre la parte inferior del bucle, y si lleva suficiente velocidad alcanzará C. La única condición es que la velocidad no debe anularse antes de llegar a C. Ponemos pues la condición crítica, que la velocidad en C sea nula. Aplicando el principio de conservación de la energía entre A y C tendremos que en A sólo hay energía cinética, y en C energía potencial. Por tanto:
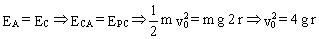
b) En cuanto a la fuerza normal en B aislamos de nuevo este cuerpo en el punto B y tendremos:
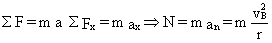
Para calcular la velocidad en B hacemos como antes, aplicamos la conservación de la energía entre los puntos A y B, teniendo en cuenta que en A tenemos sólo energía cinética, mientras que en B tenemos energía cinética y potencial:
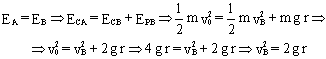
Sustituyendo este valor en la expresión de la normal tenemos: