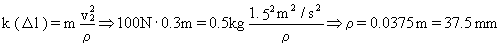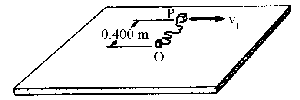a) v₁=4.50 m/s
b) v₂=1.50 m/s
c) r=37.5 mm

a y b) Hasta que el cordón alcanza su longitud natural (0.9 m), no ejercerá ninguna fuerza sobre el bloque y éste mantendrá la velocidad que tenía v₁, ya que tampoco existe rozamiento. A partir de ese momento, el cordón empieza a estirarse y por tanto el bloque estará sometido a la fuerza de recuperación del cordón, siempre dirigida hacia O. La trayectoria empezará a hacerse curvilínea. Como esta fuerza es conservativa la energía mecánica en todo instante se conserva. Si aplicamos la conservación de la energía entre el instante en que el cordón mide justo 0.9 m (1) y un instante cualquiera (2) tendremos:

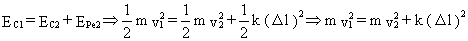
siendo v₂ la velocidad correspondiente a un determinado alargamiento del cordón Δl.

Si la distancia máxima que debe alcanzar el bloque respecto a O es de 1.2 m, el alargamiento máximo del cordón (Δl) será:

Δl=1.2-0.9=0.3 m

Además, por tratarse de una fuerza central se conserva el momento cinético o angular:

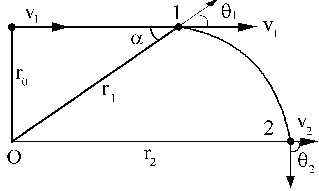
L_O=cte ⇒ L_O1=L_O2 ⇒ r₁ X mv₁=r₂ X mv₂ ⇒ mr₁v₁senθ₁=mr₂v₂senθ₂

Si estamos en la situación en que el bloque alcanza la máxima distancia de O, entonces la componente radial de la velocidad será: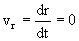 pues r tiene un valor máximo, por lo que en la situación 2 v y r son perpendiculares (sen θ₂=1). En cuanto a θ₁, que es el ángulo que forman r₁ y v₁ tendremos:

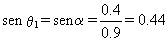
Tenemos, por tanto, un sistema de dos ecuaciones con dos incógnitas:

mv₁²=mv₂²+k(Δl)² ⇒ 0.5v₁²=0.5v₂²+100 × 0.3²

r₁v₁senθ₁=r₂v₂senθ₂ ⇒ 0.9v₁ × 0.44=1.2v₂

Resolviendo el sistema de dos ecuaciones y dos incógnitas:

v₁=4.5 m/s

v₂=1.5 m/s

c) Cuando P está a la máxima distancia de O, ya hemos dicho que v y r son perpendiculares. La única fuerza que actúa sobre P es la recuperadora del cordón, que tiene la dirección de r y sentido hacia O. Si aislamos el bloque P en esta posición y aplicamos la segunda ley de Newton tendremos:

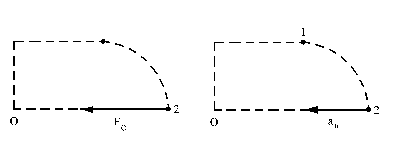
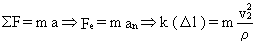
donde r
es el radio de curvatura de la trayectoria en ese punto. Sustituyendo los valores que son conocidos en la posición 2 tendremos: