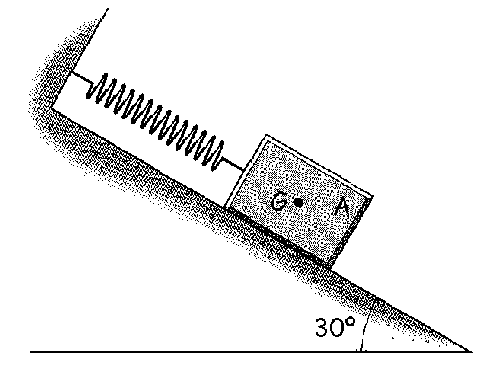
a) x_máx=8.1 m
b) v=4.02 m/s
c) t=1.68 s
d) a= 17.62 m/s²

a) En primer lugar determinaremos la masa del cuerpo, que será:

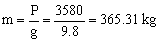
Trazamos el diagrama de sólido libre del cuerpo:

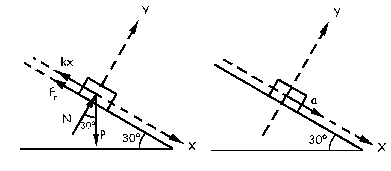
Aplicando la ecuaciones de la dinámica tendremos:

ΣF_y=0 ⇒ N-Pcos30º=0

N=Pcos30º=3580cos30º=3100.37 N

ΣF_x=ma ⇒ Psen30º-F_r-kx=ma

Como el bloque desliza:

F_r=(F_r)_máx=µN=0.1 · 3100.37=310.04 N

Por tanto en la ecuación del eje X obtenemos:

Psen30º-F_r-kx=ma ⇒ 3580sen30º-310.04-365x=365.31a

1479.96-365x=365.31a ⇒ a=4.05-x

La aceleración es la derivada de la velocidad respecto del tiempo, luego podemos escribir:

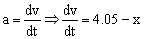
Multiplicamos y dividimos en el primer miembro por un elemento diferencial de espacio dx:

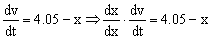
Teniendo en cuenta que:

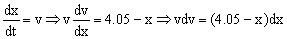
Y como tenemos las variables separadas, podemos integrar, teniendo en cuenta que en el instante inicial t=0 ⇒ x=0 ⇒ v=0:

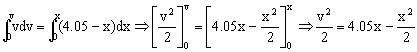
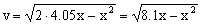
Tenemos por tanto la expresión de la velocidad en función del desplazamiento (que en este caso coincide con la elongación). El máximo desplazamiento del bloque (x_máx) coincidirá con el momento en que se detenga, es decir, la velocidad será nula:

v=0 ⇒ 8.1x_máx-x²_máx=0 ⇒ 8.1-x_máx=0

x_máx=8.1 m

b) Ahora, para x=4.5 m:

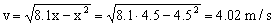
v=4.02 m/s

c) Ahora necesitamos buscar la expresión que nos dé el espacio en función del tiempo. Tendremos entonces en cuenta que la velocidad es la primera derivada del espacio respecto del tiempo:

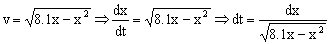
Integramos teniendo en cuenta las condiciones iniciales (cuando t=0 ⇒ x=0):

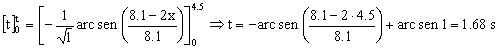
t=1.68 s

d) Cuando el bloque comienza a subir por el plano inclinado la fuerza de rozamiento y la aceleración cambian de sentido y tendremos el diagrama de sólido libre que aparece en la figura.

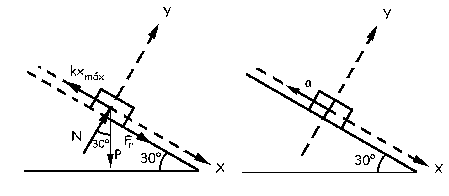
Además, el bloque empieza a subir por el plano inclinado justo cuando la elongación del muelle es la máxima. En este instante, para el eje Y:

ΣF_y=0 ⇒ N-Pcos30º=0 ⇒ N=Pcos30º=3580cos30º=3100.37 N

Y para el eje X:

ΣF_x=ma ⇒ kx_máx-F_r-Psen30º=ma ⇒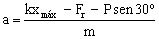

Como el bloque desliza:

F_r=(F_r)_máx=µN=0.1 · 3100.37=310.04 N

Sustituyendo:

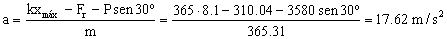
a=17.62 m/s²