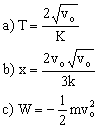
a) Trazamos en primer lugar el diagrama de sólido libre de la partícula M.
Aplicando la segunda ley de Newton:
S
Fx=ma Þ
R=ma
Teniendo en cuenta la expresión de R y que la aceleración es la derivada de la velocidad respecto del tiempo, y que en nuestro caso velocidad y aceleración tienen distinto signo:
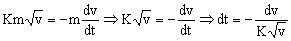
Una vez que tenemos las variables separadas, procedemos a integrar la ecuación, recordando que cuando t=0 Þ
v=v0:
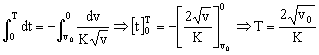
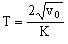
b) Volvamos ahora a la ecuación que habíamos obtenido aplicando la segunda ley de Newton, y que era:
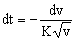
Realizamos ahora la integración para el caso más genérico, es decir, entre el tiempo t=0 (en el cual la velocidad es v0) y un tiempo genérico t para el cual la velocidad será v:
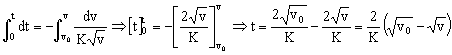
Despejamos v de esta ecuación:
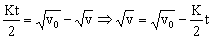
Si elevamos los dos miembros al cuadrado:
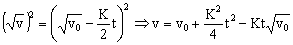
Como la velocidad es la derivada del espacio respecto del tiempo:
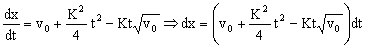
Y una vez que tenemos las variables separadas integramos la ecuación, entre el instante t=0 (donde el espacio recorrido es nulo) y t=T (donde el espacio recorrido es x):
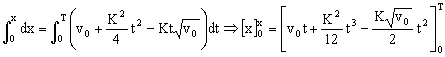
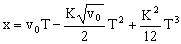
Y sustituyendo T por su valor:
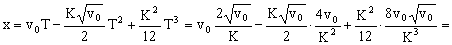
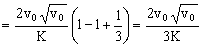
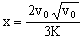
c) El trabajo realizado por la fuerza R vendrá dado por:
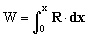
donde R es la fuerza y dx el desplazamiento de su punto de aplicación. Estos dos vectores tienen la misma dirección y sentido contrario, luego tendremos:
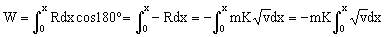
Teniendo en cuenta que:
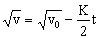
Y que:
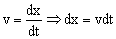
Sustituyendo todo en la ecuación del trabajo:
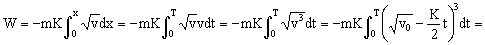
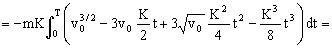
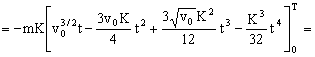
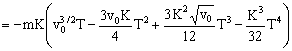
Y sustituimos el valor que hemos obtenido para T en el primer apartado:
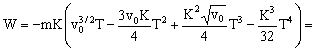
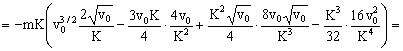
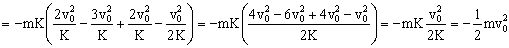
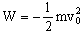
.ar79{position:absolute;clip:rect(409px,auto,auto,409px);}
.aes7{position:absolute;clip:rect(394px,auto,auto,446px);}
.aaxz{position:absolute;clip:rect(443px,auto,auto,393px);}
.at6m{position:absolute;clip:rect(426px,auto,auto,476px);}
.ajc1{position:absolute;clip:rect(392px,auto,auto,394px);}
.ajno{position:absolute;clip:rect(415px,auto,auto,396px);}
.ab9g{position:absolute;clip:rect(477px,auto,auto,463px);}
.auto{position:absolute;clip:rect(403px,auto,auto,401px);}
.ab6v{position:absolute;clip:rect(432px,auto,auto,391px);}
.af0e{position:absolute;clip:rect(424px,auto,auto,461px);}
.aag9{position:absolute;clip:rect(482px,auto,auto,417px);}
.ab5b{position:absolute;clip:rect(473px,auto,auto,470px);}
.a7so{position:absolute;clip:rect(425px,auto,auto,405px);}
.apjo{position:absolute;clip:rect(476px,auto,auto,435px);}
.ahh5{position:absolute;clip:rect(412px,auto,auto,439px);}
.arel{position:absolute;clip:rect(463px,auto,auto,477px);}
.avi5{position:absolute;clip:rect(442px,auto,auto,435px);}
.af8c{position:absolute;clip:rect(483px,auto,auto,480px);}
.a4t1{position:absolute;clip:rect(401px,auto,auto,479px);}
.aa69{position:absolute;clip:rect(449px,auto,auto,448px);}
.awee{position:absolute;clip:rect(421px,auto,auto,464px);}
.apjx{position:absolute;clip:rect(392px,auto,auto,424px);}
.avql{position:absolute;clip:rect(393px,auto,auto,482px);}
.azd4{position:a
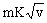 , siendo K una constante positiva dada. En el instante inicial se lanza al móvil desde O en el sentido OX con una velocidad dada v0. Se pide: a) el tiempo T transcurrido hasta que la velocidad se anula; b) el espacio recorrido durante el tiempo T; c) el trabajo realizado por la fuerza R durante el mismo tiempo T.
, siendo K una constante positiva dada. En el instante inicial se lanza al móvil desde O en el sentido OX con una velocidad dada v0. Se pide: a) el tiempo T transcurrido hasta que la velocidad se anula; b) el espacio recorrido durante el tiempo T; c) el trabajo realizado por la fuerza R durante el mismo tiempo T.