a) v₁=0.902 m/s
b) v₂=1.427 m/s
c) v_máx=1.16 m/s
d) t=1.361 s

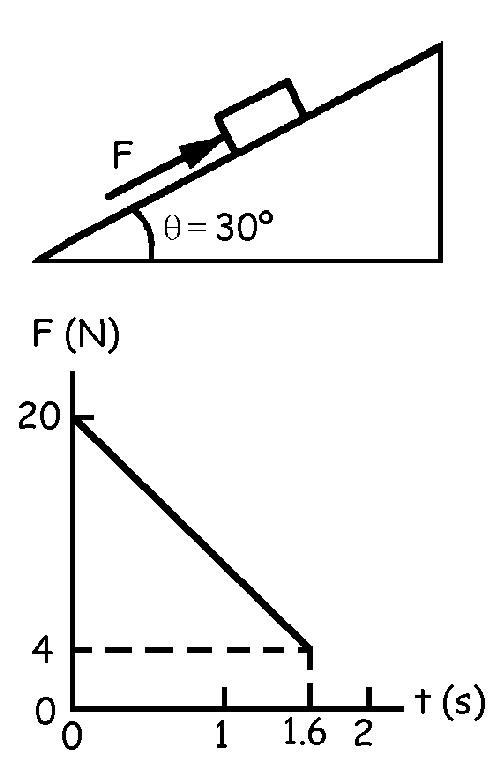
a) En primer lugar determinaremos la ecuación de la recta que nos da F en función del tiempo. Esta ecuación será del tipo:

F=a-bt

Conocemos dos puntos de esta recta:

t=0 ⇒ F=20 N ⇒ F=a-bt ⇒ 20=a

t=1.6 ⇒ F=4 N ⇒ F=a-bt ⇒ 40=20-1.6b ⇒ b=10

Luego la ecuación de la fuerza F es:

F=a-bt=20-10t

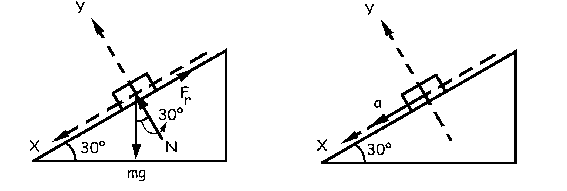
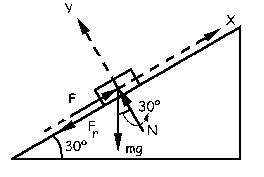Ahora tendremos que desde t=0 hasta t=1.6 s sobre el cuerpo se aplican las fuerzas que aparecen en el diagrama. El movimiento se produce únicamente en el eje X. Tendremos entonces:

ΣF_y=0 ⇒ N-mgcos30^O=0

N=mgcos30^O=2 · 9.8cos30^O=16.97 N

Como el cuerpo desliza la fuerza de rozamiento adquiere su valor máximo:

F_r=(F_r)_máx=µN=0.2 · 16.97=3.39 N

Las fuerzas aplicadas en el eje X son:

ΣF_x=F-F_r-mgsen30^O=20-10t-3.39-2 · 9.8sen30^O=6.805-10t

Como t=1 s está dentro del intervalo en que se aplica la fuerza F, podemos aplicar el teorema del impulso al eje X, que es el único eje en el que hay movimiento. Teniendo en cuenta que el bloque parte del reposo:

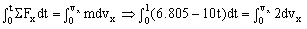
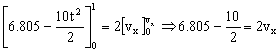
v_x=0.902 m/s

b) Ahora para t=2 s está fuera del intervalo en que actúa la fuerza F. Dividiremos el movimiento en dos partes, desde t=0 hasta t=1.6 s tendremos las mismas fuerzas que antes, y desde t=1.6 s hasta t=2 s determinaríamos la velocidad final de otra forma, ya que la fuerza F no actuaría. En el primer tramo tendremos:

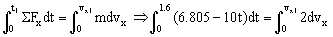
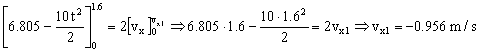
Como la velocidad es negativa, significa que el bloque en ese momento se está moviendo hacia abajo. Lo que hemos hecho entonces no es válido, ya que si durante un cierto tiempo el bloque se mueve hacia abajo la fuerza de rozamiento cambia de sentido y el sumatorio de fuerzas en el eje X sería distinto. Debemos determinar en primer lugar el momento en que el bloque cambia su sentido. En el punto en que el bloque cambia de sentido su velocidad pasa de ser positiva a negativa, luego en ese instante tiene que ser nula. Llamaremos t₀ al instante en que la velocidad se anula. Tendremos:

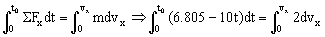
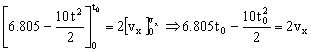
Si la velocidad se anula:

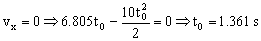
Obtenemos además otra solución que es t₀=0, que descartamos porque sería el instante inicial en que empieza el movimiento desde el reposo. Tendremos entonces que desde t=0 hasta t₀=1.361 s el bloque se mueve hacia arriba como antes, y en ese instante se detiene:

v_x0=0

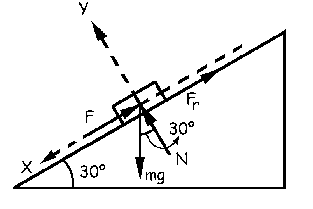Desde t₀=1.361 s hasta t₁=1.6 s el bloque se mueve hacia abajo, por lo que el sistema de fuerzas sería ahora el que aparece en la figura. Tendremos:

ΣF_y=0 ⇒ N-mgcos30^O=0

N=mgcos30^O=2 · 9.8cos30^O=16.97 N

Como el cuerpo desliza la fuerza de rozamiento adquiere su valor máximo:

F_r=(F_r)_máx=µN=0.2 · 16.97=3.39 N

Las fuerzas aplicadas en el eje X son:

ΣF_x=mgsen30^O-F-F_r=2 · 9.8sen30^O-20+10t-3.39=10t-13.59

Aplicando el teorema del impulso a este intervalo:

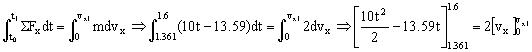
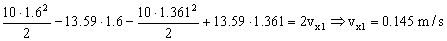
Desde t=1.6 s hasta t=2 s la fuerza F deja de actuar y el bloque resbala libremente por el plano inclinado. Tendremos entonces:

F_y=0 ⇒ N-mgcos30^O=0 ⇒ N=mgcos30^O=2 · 9.8cos30^O=16.97 N

F_r=(F_r)_máx=µN=0.2 · 16.97=3.39 N

ΣF_x=ma ⇒ mgsen30^O-F_r=ma ⇒ 2 · 9.8sen30^O-3.39=2a ⇒ a=3.205 m/s²

La aceleración es constante, luego en este intervalo el movimiento es rectilíneo uniformemente acelerado durante un período de tiempo de:

t=2-1.6=0.4 s

Aplicando la ecuación del movimiento uniformemente acelerado:

v_x2=v_x1+at=0.145+3.205 · 0.4=1.427 m/s

v_x2=1.427 m/s

c) Si la velocidad máxima se alcanza subiendo, tendremos que debe ocurrir entre t=0 y t=1.361 s, que es el intervalo de tiempo en que el bloque está subiendo. En este tramos las fuerzas que actuaban sobre el bloque en el eje X eran:

ΣF_x=6.805-10t

Por tanto aplicando el teorema del impulso:

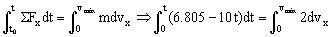
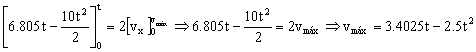
Como la velocidad es máxima su derivada debe ser nula:

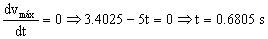
Con este tiempo tendremos que la velocidad máxima es:

v_máx=3.4025t-2.5t²=3.4025 · 0.6805-2.5 · 0.6805²=1.16 m/s

v_máx=1.16 m/s

d) El tiempo en que el bloque se detiene ya lo hemos determinado en el apartado b) luego es:

t₀=1.361 s

Desde t₀=1.361 s hasta t=1.6 s el bloque baja por el plano inclinado acelerando pero con una aceleración variable, ya que la fuerza F varía con el tiempo. A partir de t=1.6 s la fuerza F desaparece y el bloque sigue moviéndose hacia abajo por el plano inclinado únicamente bajo la acción de su peso y la fuerza de rozamiento. A partir de t=1.6 s las fuerzas que actúan sobre el bloque son constantes, lo que implica que la aceleración es constante y habría movimiento rectilíneo uniformemente acelerado con a=3.205 m/s².