a) t=0.206 s
b) v_pelota=-1.819 m/s; v_piedra=22.98 m/s
c) t_pelota=2.04 s; t_piedra=5.10 s

a) En los dos casos el movimiento es rectilíneo uniformemente acelerado. Representaremos a la pelota con el subíndice 1 y a la piedra con el subíndice 2. Las velocidades iniciales en los dos casos son:

v₀₁=10 m/s; v₀₂=25 m/s

En los dos casos la aceleración es la de la gravedad, y mientras que la pelota está en el aire un tiempo t, la piedra estará en el aire un tiempo t-1. Cuando se crucen ambas estarán a la misma altura. Para la pelota:

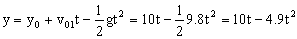
Y para la piedra:

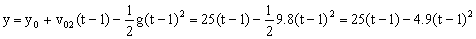
Igualando las dos expresiones:

10t-4.9t²=25(t-1)-4.9(t-1)² ⇒ 10t-4.9t²=25t-25-4.9t²-4.9+9.8t ⇒ 29.9-24.8t=0

Por tanto el tiempo que tardan en estar ambas a la misma altura es:

t=1.206 s

Hemos llamado t al tiempo que la pelota está en el aire. La piedra por tanto estará un tiempo t-1:

t₂=t-1=1.206-1=0.206 s

t₂=0.206 s

b) La velocidad de la pelota será:

v_F1=v₀₁-gt=10-9.8 · 1.206=-1.819 m/s

v_F1=-1.819 m/s

Y la de la piedra:

v_F2=v₀₂-gt₂=25-9.8 · 0.206=22.98 m/s

v_F2=22.98 m/s

Los distintos signos implican que la pelota está ya bajando, mientras que la piedra todavía está subiendo.

c) Cuando los objetos estén otra vez en el suelo, la velocidad con que llegan a él es la misma que la inicial pero con distinto signo. Por tanto para la pelota:

v_F1=v₀₁-gt₁ ⇒ -10=10-9.8t₁ ⇒ 9.8t₁=20

t₁=2.04 s

Y para la piedra:

v_F2=v₀₂-gt₂ ⇒ -25=25-9.8t₂ ⇒ 9.8t₂=50

t₂=5.10 s