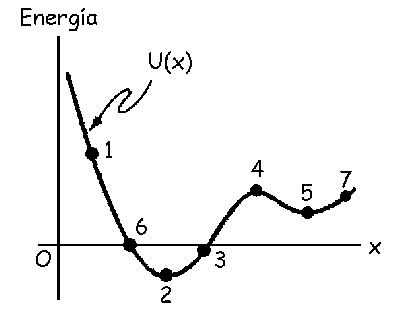
a) puntos 1 y 6: positiva; punto 3: negativa; puntos 2,4 y 5: nula
b) punto 1: mas positiva, punto 3: mas negativa; puntos 2, 4 y 5: nula
c) puntos 2 y 5: equilibrio estable; punto 4: equilibrio inestable
a) Como el campo de fuerzas es conservativo:
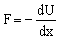
Geométricamente, la derivada es la pendiente de la tangente en el punto dado. Como tenemos un signo negativo, la fuerza tendrá signo contrario al de la pendiente de la tangente. Entonces, en los puntos 1 y 6 la pendiente es negativa luego la fuerza es positiva:
PUNTOS 1 y 6: POSITIVA
En el punto 3 la pendiente es positiva luego la fuerza es negativa:
PUNTOS 3 y 7: NEGATIVA
En los puntos 2, 4 y 5 la tangente es horizontal, luego la pendiente, y por tanto la fuerza, es nula:
PUNTOS 2, 4 y 5: NULA
b) La fuerza y la pendiente de la tangente tienen signo contrario, lo que implica que la fuerza es más positiva donde la pendiente es más negativa y viceversa. Entre los puntos 1 y 6, en valor absoluto la pendiente es mayor en el punto 1. Las pendientes son negativas luego la fuerza es positiva, y es más positiva en el punto 1.
PUNTO 1: MÁS POSITIVA
Entre los puntos 3 y 7, en valor absoluto, la pendiente es mayor en el punto 3, luego:
PUNTO 3: MÁS NEGATIVA
La fuerza es nula donde la tangente es horizontal, es decir, en los puntos 2, 4 y 5:
PUNTOS 2, 4 y 5: NULA
c) Las posiciones de equilibrio coinciden con aquéllas en las que la fuerza es nula, luego serían las correspondientes a los puntos 2, 4 y 5:
EQUILIBRIO: PUNTOS 2, 4 y 5
Veamos ahora qué tipo de equilibrio tienen estos puntos. Empecemos por el punto 4. Supongamos que desplazamos la partícula de la posición de equilibrio, por ejemplo, hacia la izquierda, es decir, en sentido negativo. La pendiente de la tangente entonces es positiva, lo que implica que la fuerza, que tiene signo contrario, es negativa, es decir, como el desplazamiento. Aparecería una aceleración en el mismo sentido que haría alejarse a la partícula cada vez más de la posición de equilibrio. Tendríamos entonces que el punto 4 es un punto de equilibrio inestable, ya que al separar ligeramente a la partícula de la posición de equilibrio, ésta tiene a alejarse cada vez más de dicho punto
PUNTO 4: EQUILIBRIO INESTABLE
Veamos ahora el punto 2. Supongamos que desplazamos la partícula del punto 2 hacia la izquierda (sentido negativo). La pendiente de la tangente es entonces negativa, y la fuerza, que tiene signo contrario, es positiva. Aparece por tanto una fuerza de sentido contrario al desplazamiento que tiende a hacer regresar a la partícula a su posición de equilibrio. Este punto sería por tanto un punto de equilibrio estable, ya que al alejar a la partícula de su posición de equilibrio ésta tiende a volver a él. Lo mismo ocurriría con el punto 4.
PUNTOS 2 y 4: EQUILIBRIO ESTABLE