v1´=3.99 m/s; v2´= 3.01
 Llamaremos 1 al disco azul y 2 al amarillo. Podemos hacer un gráfico con las velocidades antes y después del choque, y elegir un sistema de ejes coordenados adecuado, haciendo coincidir el eje X con la dirección inicial del movimiento del disco azul. Se debe conservar la cantidad de movimiento en los dos ejes, de manera que tendremos:
Llamaremos 1 al disco azul y 2 al amarillo. Podemos hacer un gráfico con las velocidades antes y después del choque, y elegir un sistema de ejes coordenados adecuado, haciendo coincidir el eje X con la dirección inicial del movimiento del disco azul. Se debe conservar la cantidad de movimiento en los dos ejes, de manera que tendremos:
EJE X: pantes=pdespués ⇒ mv1=mv1´cos37º+mv2´cos53º ⇒ v1=v1´cos37º+v2´cos53º
5=v1´cos37º+v2´cos53º
EJE Y: pantes=pdespués ⇒ 0=mv1´sen37º-mv2´sen53º ⇒ 0=v1´sen37º-v2´sen53º
De la ecuación del eje Y:
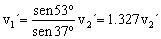
Y sustituyendo en la ecuación del eje X:
5=v1´cos37º+v2´cos53º ⇒ 5=1.327v2´cos37º+v2´cos53º ⇒ 5=1.662v2´
v2´=3.01 m/s
Con lo cual la velocidad del otro disco:
v1´=1.662v2´=1.662 · 3.01=3.99 m/s
v1´=3.99 m/s