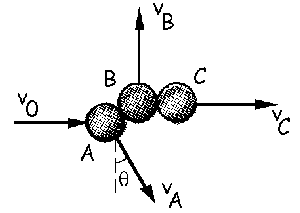
vA=1.5 m/s; vB=1.299 m/s; vC=2.25 m/s
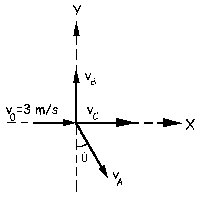 Tomamos un sistema de ejes coordenados como el que aparece en la figura. Como el choque es perfectamente elástico se conservará la cantidad de movimiento en los dos ejes y la energía cinética. Tendremos las ecuaciones:
Tomamos un sistema de ejes coordenados como el que aparece en la figura. Como el choque es perfectamente elástico se conservará la cantidad de movimiento en los dos ejes y la energía cinética. Tendremos las ecuaciones:
(px)antes=(px)después
(py)antes=(py)después
(EC)antes=(EC)después
Desarrollando las ecuaciones:
mv0=mvAsen30º+mvC
0=mvB-mvAcos30º
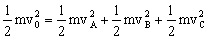
Simplificando las masas que son iguales y sustituyendo los valores conocidos:
3=0.5vA+vC
0=vB-0.866vA
9=vA2+vB2+vC2
De la segunda ecuación:
vB=0.866vA
Sustituyendo en las otras dos:
3=0.5vA+vC ⇒ 3=0.5vA+vC
9=vA2+vB2+vC2 ⇒ 9=vA2+(0.866vA)2+vC2
Ahora de la primera ecuación:
3=0.5vA+vC ⇒ vC=3-0.5vA
Y sustituyendo en la otra:
9=vA2+(0.866vA)2+vC2 ⇒ 9=vA2+0.75vA2+(3-0.5vA)2 ⇒ 9=1.75vA2+9+0.25vA2-3vA ⇒ 2vA2-3vA=0
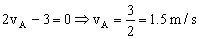
vA=1.5 m/s
vC=3-0.5vA=3-0.5 · 1.5=2.25 m/s
vC=2.25 m/s
vB=0.866vA=0.866 · 1.5=1.299 m/s
vB=1.299 m/s