a) v1´=1.084 m/s; v2´=4.336 m/s
b) h=0.240 m
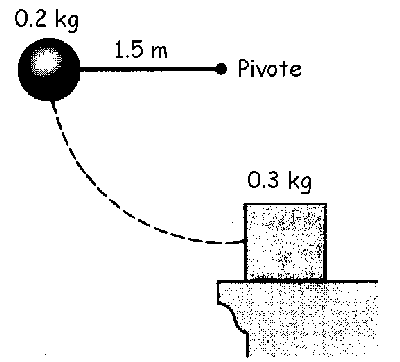
a) Denominaremos con el subíndice 1 a la bola, y con el subíndice 2 al bloque. Para el péndulo tendremos que se conserva la energía entre la posición más alta y la más baja de la trayectoria. Por tanto:
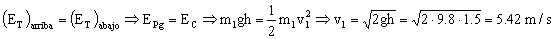
La bola choca contra el bloque en reposo con una velocidad de 5.42 m/s. Como el choque es elástico se conservan la cantidad de movimiento y la energía cinética entre antes y después del choque:
Pantes=pdespués ⇒ 1v1=m1v1´+m2v2´
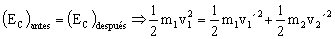
Simplificando:
0.2 · 5.42=0.2v1´2+0.3v2´2 ⇒ 1.084=0.2v1´+0.3v2´
0.2 · 5.422=0.2v1´2+0.3v2´2 ⇒ 5.87528=0.2v1´2+0.3v2´2
De la primera ecuación:
1.084=0.2v1´+0.3v2´ ⇒ v1´=5.42-1.5v2´
Y sustituyendo en la segunda:
5.87528=0.2v1´2+0.3v2´2 ⇒ 5.87528=0.2(5.42-1.5v2´)2+0.3v2´2
5.87528=5.87528+0.45v2´2-3.252v2´+0.3v2´2 ⇒ 0=0.45v2´2-3.252v2´+0.3v2´2
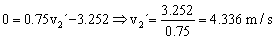
v2´=4.336 m/s
Y la otra velocidad:
v1´=5.42-1.5v2´=5.42-1.5 · 4.336=-1.084 m/s
v1´=-1.084 m/s
El signo negativo implica que la bola se mueve en sentido contrario al inicial.
b) Ahora, exactamente igual que antes, la bola llega a la parte más baja de su trayectoria y choca contra el bloque con una velocidad de 5.42 m/s. Después, como el choque es inelástico, los dos cuerpos permanecen unidos y se mueven con una misma velocidad v. El momento lineal antes y después del choque permanece constante:
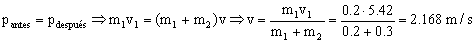
Ahora, después del choque, se conserva la energía entre la posición más baja y la más alta de la trayectoria del centro de masa:
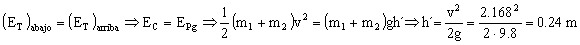
h=0.240 m