a) v1´=-2.49 m/s; v2´=7.42 m/s
b) h´=0.316 m
c)e=0.826
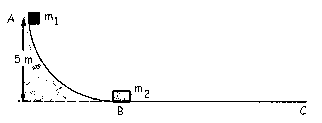
a) Antes del choque, para el bloque m1 se conserva la energía total:
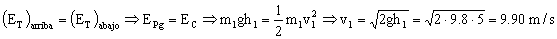
El bloque m1 choca contra el bloque m2 que está en reposo con una velocidad de 9.90 m/s. Como el choque es elástico, se conservan tanto la cantidad de movimiento como la energía total:
pantes=pdespués ⇒1v1=m1v1´+m2v2´
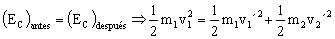
Simplificando y sustituyendo los valores conocidos:
6 · 9.90=6v1´+10v2´ ⇒ 59.40=6v1´+10v2´
6 · 9.902=6v1´2+10v2´2 ⇒ 588=6v1´2+10v2´2
De la primera ecuación:
59.40=6v1´+10v2´ ⇒ v1´=9.90-1.67v2´
Y sustituyendo en la segunda:
588=6v1´2+10v2´2 ⇒ 588=6(9.90-1.67v2´)2+10v2´2 ⇒ 588=588+16.67v2´2-198v2´+10v2´2
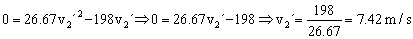
v2´=7.42 m/s
Y para el otro bloque:
v1´=9.90-1.67v2´=9.90-1.67 · 7.42=-2.49 m/s
v1´=-2.49 m/s
b) El signo negativa de esta velocidad implica que el bloque m1 se desplaza en sentido contrario y vuelve hacia arriba. A continuación se conservaría la energía total para este bloque entre esta posición en la parte más baja de la trayectoria, y la posición más alta a la que llegue:
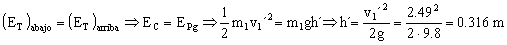
h´=0.316 m
c) Ahora tendremos que rehacer el problema al revés. Tenemos que el bloque m1 después del choque llega hasta una altura de 0.1 m. Por conservación de la energía podemos determinar cuál era su velocidad después del choque:
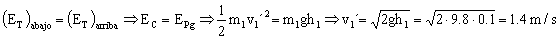
La velocidad de m1 después del choque es de 1.4 m/s (hacia la izquierda, es decir, con signo negativo). Antes del choque, el bloque m1 cae desde una altura de 5 m, luego llega hasta el bloque m2 con una velocidad que ya habíamos calculado al principio del problema, y que era:
v1=9.90 m/s
En el choque se conserva el momento cinético, luego también podemos determinar la velocidad del bloque m2 después del choque:
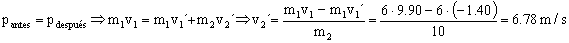
Y el coeficiente de restitución entonces:
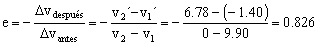
e=0.826