a)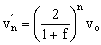
b) m_n=0.122m_o; v_n´=2.79 v_o; (E_c)_n=0.946(E_c)_o

a) En cada choque se debe conservar la cantidad de movimiento y el coeficiente de restitución debe ser 1, ya que los choques son perfectamente elásticos. Inicialmente antes del primer choque sólo se mueve la masa m₀ con velocidad v₀ (tomaremos como positivo el sentido hacia la derecha). Después del choque la bola m₀ tendrá una velocidad v₀´ hacia la izquierda y la bola fm₀ tendrá una velocidad v₁´ hacia la derecha. Aplicando a este choque las dos condiciones antes mencionadas:

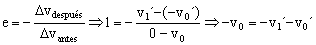
p_antes=p_después ⇒ m₀v₀=-m₀v₀´+fm₀v₁´ ⇒ v₀=-v₀´+fv₁´

De la primera ecuación:

-v₀=-v₁´-v₀´ ⇒ v₀´=v₀-v₁´

Y sustituyendo en la segunda:

v₀=-v₀´+fv₁´ ⇒ v₀=-v₀+v₁´+fv₁´ ⇒ 2v₀=v₁´(1+f) ⇒

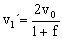
En el segundo choque pasa exactamente lo mismo. Antes del choque la bola fm₀ tiene una velocidad v₁´ hacia la derecha y choca contra la bola f²m₀ que está en reposo. Después del choque la bola fm₀ tendrá una velocidad v₁´´ hacia la izquierda y la bola f²m₀ tendrá una velocidad v₂´ hacia la derecha. Aplicando la conservación del momento lineal y el coeficiente de restitución:

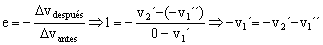
p_antes=p_después ⇒ fm₀v₁´=-fm₀v₁´´+f²m₀v₂´ ⇒ v₁´=-v₁´´+fv₂´

De la primera ecuación:

-v₁´=-v₂´-v₁´´ ⇒ v₁´´=v₁´-v₂´

Y sustituyendo en la segunda:

v₁´=-v₁´´+fv₂´ ⇒ v₁´=-v₁´+v₂´+fv₂´ ⇒ 2v₁´=v₂´(1+f) ⇒

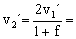
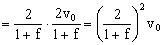
Y así sucesivamente hasta la n-ésima bola para la cual:

 

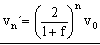
b) La masa de la última bola será:

m₂₀=fⁿm₀=0.9²⁰m₀=0.122m₀

m_n=0.122m₀

La velocidad será:

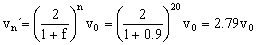
v_n´=2.79v₀

La energía cinética de la bola inicial es:

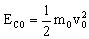
Luego la de la bola n-ésima:

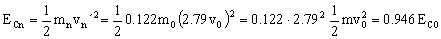
E_Cn=0.946E_Co

La energía que falta correspondería a choques secundarios y al movimiento del resto de las bolas.