ω=24 rad/s; M=0.4 m N
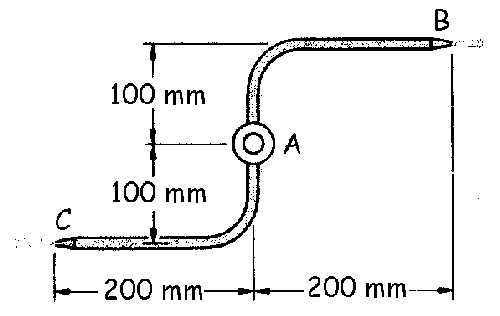
a) Tomaremos como sistema de ejes unos ejes cartesianos normales, con el eje X horizontal y positivo hacia la derecha, el eje y vertical y positivo hacia arriba y el eje Z perpendicular a los anteriores.
En primer lugar y teniendo en cuenta que la densidad del agua es 1 kg/l el flujo másico es:
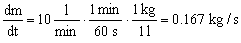
 La velocidad relativa tendrá la dirección del brazo. Necesitamos determinar la velocidad absoluta del agua en la parte de arriba (que llamaremos vB) y la velocidad absoluta del agua en la parte de abajo (que llamaremos vC). Como el aspersor es un sistema de referencia en rotación:
La velocidad relativa tendrá la dirección del brazo. Necesitamos determinar la velocidad absoluta del agua en la parte de arriba (que llamaremos vB) y la velocidad absoluta del agua en la parte de abajo (que llamaremos vC). Como el aspersor es un sistema de referencia en rotación:
vB=vA+ω
X AB+vr=ω
X AB+vr=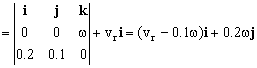
La velocidad en el punto C será igual a –vB.
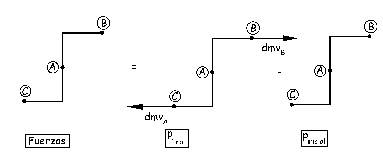 Aplicaremos ahora el teorema del impulso angular. En un tiempo t entra una masa dm a velocidad v en dirección perpendicular al plano del dibujo. No lo representaremos en el gráfico porque esta cantidad de movimiento no da momento respecto de un eje Z que pase por A, ya que sería paralelo a él. En un tiempo t+dt saldría por los dos brazos del aspersor una masa dm a velocidad vB. Tendríamos entonces:
Aplicaremos ahora el teorema del impulso angular. En un tiempo t entra una masa dm a velocidad v en dirección perpendicular al plano del dibujo. No lo representaremos en el gráfico porque esta cantidad de movimiento no da momento respecto de un eje Z que pase por A, ya que sería paralelo a él. En un tiempo t+dt saldría por los dos brazos del aspersor una masa dm a velocidad vB. Tendríamos entonces:
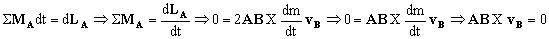
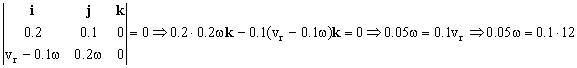
ω=24 rad/s
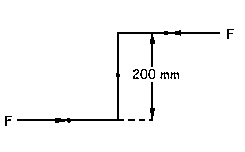 b) Para que el aspersor no gire tendremos que aplicar dos fuerzas F a sus brazos de modo que contrarresten la salida del agua. Dichas fuerzas valdrán:
b) Para que el aspersor no gire tendremos que aplicar dos fuerzas F a sus brazos de modo que contrarresten la salida del agua. Dichas fuerzas valdrán:
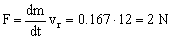
Y entonces el par:
M=Fd=2·0.2=0.4 Nm
M=0.4 Nm