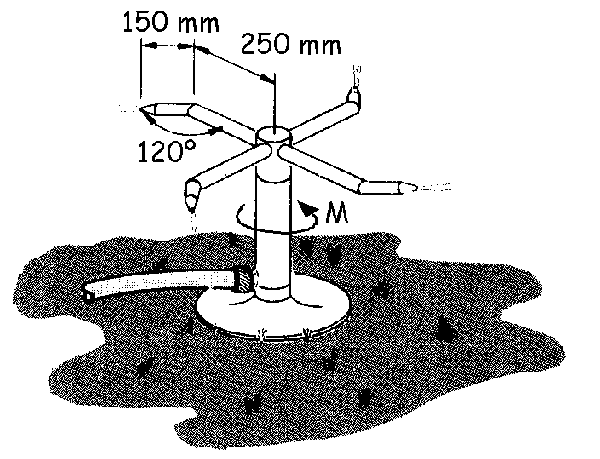
ω=23.71 rad/s
Teniendo en cuenta que la densidad del agua es de 1 kg/l el flujo másico es:
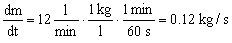
Determinaremos primero los ángulos y dimensiones de los brazos. Conocemos:
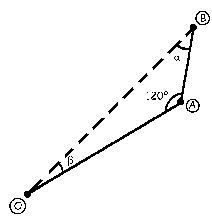 OA=0.25 m; AB=0.150 m
OA=0.25 m; AB=0.150 m
Por el teorema del coseno:
OB2=OA2+AB2-2·OA·AB cos120º
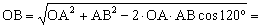

Para los ángulos utilizamos el teorema del seno:
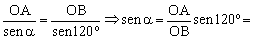
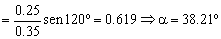
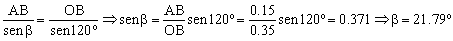
Si aplicamos el teorema del impulso, teniendo en cuenta que tenemos cuatro brazos exactamente iguales:
ΣMOdt=4dLO ⇒ ΣMOdt=4(r X dp) ⇒ ΣMOdt=4(r X dmv) ⇒ ΣMOdt=4dm(r X v)
Dividiendo los dos miembros por dt:
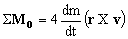
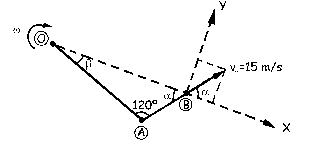 Vamos a determinar r y v, ya que el único momento respecto del punto O sería el producido por la fuerza de rozamiento:
Vamos a determinar r y v, ya que el único momento respecto del punto O sería el producido por la fuerza de rozamiento:
ΣMO=0.275k
Hemos tomado el eje Z perpendicular a los ejes X e Y.
Para la velocidad relativa tendremos:
vr=15cosα
i+15senα
j=15cos38.21ºi+15sen38.21ºj=11.79i+9.28j
La velocidad angular:
ω=-ωk
Y el vector de posición:
r=OB=0.35i
Por tanto la velocidad absoluta del agua, teniendo en cuenta que el aspersor es un sistema de referencia en rotación, será:
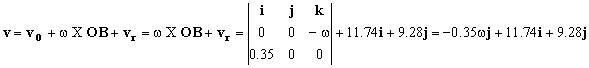
Entonces tendremos:
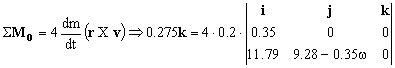
0.275k=0.8·0.35(9.28-0.35ω)k ⇒ 0.275=0.8 · 0.35(9.28-0.35ω) ⇒ 0.275=2.5824-0.098ω
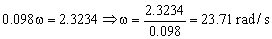
ω=23.71 rad/s