a) Δt=0.068 s
b) vmáx=32 m/s
a) La ecuación del movimiento será del tipo:
x=Asen(ωt+φ0)
donde A es la amplitud del movimiento, ω la frecuencia angular y φ 0 el ángulo de fase inicial. La amplitud es la máxima elongación, luego valdrá:
A=8 m
La frecuencia angular la podemos determinar a partir de la ecuación diferencial del movimiento, teniendo en cuenta que es:
![]()
Por comparación con la ecuación general del movimiento, que es:
![]()
obtenemos la frecuencia angular:
ω2=16 ⇒ ω=4 rad/s
Y el ángulo de fase inicial lo podemos determinar con las condiciones iniciales. Sabemos que cuando t=0 ⇒ x=0 luego sustituyendo esto en la ecuación del movimiento:
x=Asen(ωt+φ0) ⇒ 0=Asenφ0 ⇒ senφ0=0 ⇒ φ0=0
Tendremos entonces que la solución del movimiento es:
x=Asen(ωt+φ0)=8sen4t
Para los puntos conocidos tenemos:
x1=2 m ⇒ 2=8sen4t1 ⇒ t1=0.063 s
x2=4 m ⇒ 4=8sen4t1 ⇒ t2=0.131 s
El intervalo de tiempo es entonces:
Δt=t2-t1=0.131-0.063=0.068 s
Δt=0.068 s
b) La velocidad será:

El único término variable de esa ecuación es el coseno, luego la velocidad será máxima cuando el coseno adquiera su valor máximo, que es la unidad:
cos4t=1 ⇒ vmáx=32 m/s
vmáx=32 m/s
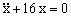 , donde
, donde 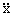 es la aceleración del movimiento. Determinar: a) tiempo que transcurre para que el punto se desplace desde la posición x=2 m a x=4 m, si el valor máximo que puede alcanzar x es de 8 m, y cuando t=0 ⇒ x=0; b) velocidad máxima que puede alcanzar dicho punto material.
es la aceleración del movimiento. Determinar: a) tiempo que transcurre para que el punto se desplace desde la posición x=2 m a x=4 m, si el valor máximo que puede alcanzar x es de 8 m, y cuando t=0 ⇒ x=0; b) velocidad máxima que puede alcanzar dicho punto material.