a) ω=15.81 rad/s
b) y=0.0523 m
c) A=0.0131 m; φo=180o
a) En la frecuencia angular sólo intervienen la constante del resorte y la masa del cuerpo luego:
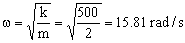
ω=15.81 rad/s
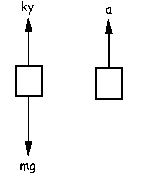
b) Tomaremos a partir de aquí el eje X como eje horizontal, y el eje Y como el vertical. Cuando el sistema está acelerando tendremos los diagramas que aparecen en la figura. Aplicando la segunda ley de Newton:
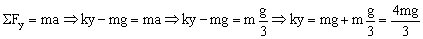
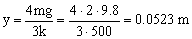
y=0.0523 m
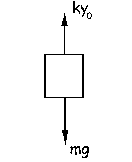 c) Para la posición de equilibrio tendremos lo que aparece en la figura:
c) Para la posición de equilibrio tendremos lo que aparece en la figura:
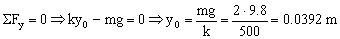
El sistema está en equilibrio cuando el resorte está estirado 0.0392 m, y sabemos que se estira hasta 0.0523 m. Como la amplitud se cuenta con respecto a la posición de equilibrio:
A=y-y0=0.0523-0.0392=0.0131 m
A=0.0131 m
Para un observador que se encuentre en el ascensor la ecuación del movimiento del cuerpo será:
y=Asen(ωt+φ0)
El ascensor inicia su movimiento cuando el cuerpo está en la posición de equilibrio, es decir:
t=0 ⇒ y=0 ⇒ 0=Asenφ0 ⇒ senφ0=0 ⇒ φ0=0 ó 180º
Además, para un observador situado en el ascensor, cuando el ascensor se empieza a mover hacia arriba el cuerpo se desplaza hacia abajo, luego la velocidad debe ser negativa. La velocidad valdrá:

En el instante inicial, cuando t=0:
v=Aωcosφ0
Para que esta velocidad sea negativa y además senφ0=0 deberá verificarse que:
cosφ0=-1 ⇒ φ0=180º
φ0=180º