Problema de Movimiento Oscilatorio

Una canica de masa m=50 g resbala sin rozamiento en el fondo de un cuenco semiesférico de radio R=20 cm. En el instante t=0 se suelta la canica partiendo del reposo desde un ángulo θ=0.1 rad (ver figura). Admitiendo que se mueve en un plano vertical que pasa por el fondo del cuenco: a) deducir la ecuación que describe el movimiento de la canica; b) calcular la frecuencia de las oscilaciones; c) ¿cuál es la energía total del sistema? d) ¿cuál es la velocidad de la canica cuando t=0.1 s? e) ¿cuál es su aceleración cuando t=0.2 s? f) Consideremos ahora que la canica describa un movimiento circular respecto al eje de simetría del cuenco y a una altura pequeña respecto al fondo. Determinar el tiempo que tarda en recorrer una vuelta.

a) 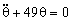; θ=0.1cos7t
b) ω=7 rad/s
c) E=0.0049 J
d) v=0.09 m/s
e) a=0.192 m/s2
f) t=0.898 s

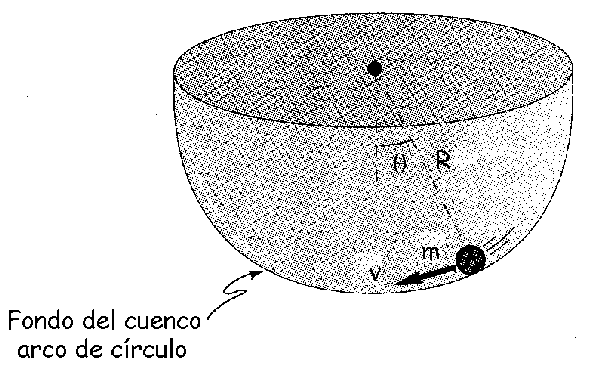
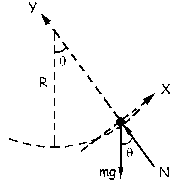a) Aislamos la partícula, tal como se ve en la figura. En el eje X tendremos la aceleración tangencial, y en el eje Y la normal. Para el eje X, aplicando la segunda ley de Newton:

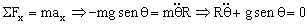
Para pequeñas oscilaciones el ángulo θ es muy pequeño y podemos realizar la aproximación:

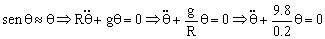
Tenemos que es la ecuación de un movimiento armónico simple de frecuencia angular:

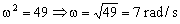
La solución de la ecuación diferencial será por tanto del tipo:

θ=θ0sen(ωt+φ0)=0.1sen(7t+φ0)

De las condiciones iniciales sabemos que cuando t=0 ⇒ θ=θ0=0.1 rad, luego aplicando esta condición:

θ=0.1sen(7t+φ0) ⇒ 0.1=0.1senφ0 ⇒ senφ0=1 ⇒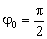

Nos queda la ecuación:

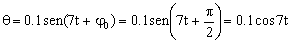
θ=0.1cos7t

 

b) Ya hemos determinado antes la frecuencia angular:

ω=7 rad/s

 

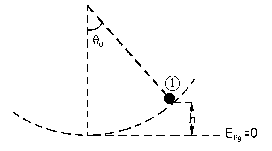c) La energía total se mantiene constante, luego puedo determinarla en cualquier punto. Tomamos el punto que denominaremos 1, en el cual se suelta la bolita desde el reposo formando un ángulo con la vertical de θ0=0.1 rad.

La energía total será:

ET=ET1=EPg1=mgh=mg(R-Rcosθ)=5·10-2 · 9.8(0.2-0.2cos0.1)=0.0049 J

ET=0.0049 J

 

d) La velocidad angular es la derivada del ángulo respecto del tiempo luego:

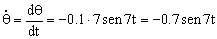
Para t=0.1 s:

Como la partícula realiza un movimiento circular, la velocidad lineal será:

v=0.2 · 0.45=0.09 m/s

v=0.09 m/s

 

e) Ahora la aceleración angular es la derivada de la velocidad angular respecto del tiempo:

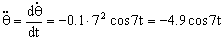
Para t=0.2 s:

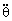=-4.9cos7t=-4.9cos(7 · 0.2)=-0.833 rad/s2

 

Como la partícula realiza un movimiento circular tendremos dos componentes de aceleración, la tangencial y la normal. La aceleración tangencial vale:

Y la aceleración normal será:

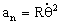
Necesitamos la velocidad angular cuando t=0.2 s, que es:

Luego la aceleración normal es:

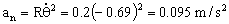
Como las aceleraciones tangencial y normal tienen direcciones perpendiculares, la aceleración total es:

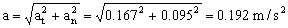
a=0.192 m/s2

 

f) El movimiento en este caso es la superposición de dos movimientos armónicos simples perpendiculares, uno como el del apartado a) y otro en dirección perpendicular. Por tanto el período es el mismo que antes, y el tiempo que tarda la partícula en dar una vuelta completa es el período. Tendremos:

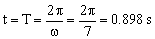
t=0.898 s