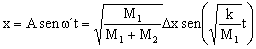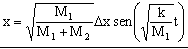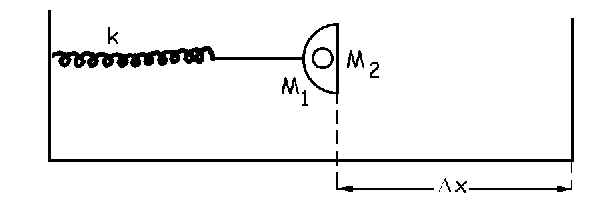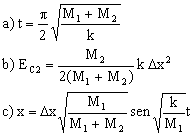
a) La bola y la copa comenzarán a separarse al pasar por la posición de equilibrio, ya que a partir de ahí el resorte empieza a estar estirado ejerciendo una fuerza sobre la copa, en sentido opuesto al desplazamiento, por lo cual la copa empezaría a disminuir su velocidad, mientras que la bola no por no estar unida al resorte. El tiempo que transcurre desde la posición de máxima elongación hasta la posición de equilibrio es la cuarta parte del período. El período vale:

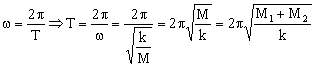
Entonces el tiempo que tarda la copa en llegar a esa posición es:

 

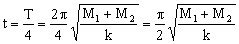
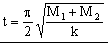
b) La energía se conserva durante el movimiento conjunto de la bola y la copa, de modo que la energía potencial elástica correspondiente a la máxima compresión debe transformarse íntegramente en energía cinética al pasar por la posición de equilibrio. En este caso:

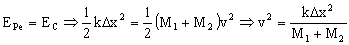
Hemos determinado entonces la velocidad que tienen tanto la bola como la copa en el instante de la separación. La energía cinética correspondiente a la bola será:

 

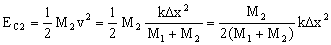
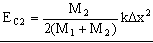
c) En el momento de la separación la energía cinética correspondiente a la copa es:

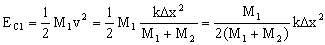
A partir de este momento la energía total del sistema muelle-copa se conserva. La energía cinética entonces empieza a disminuir, transformándose en energía potencial elástica. Cuando el sistema quede estirado una cantidad Δx´, siendo Δx´ la amplitud del nuevo movimiento vibratorio, el sistema quedará momentáneamente en reposo. Aplicando la conservación de la energía entre estos dos momentos:

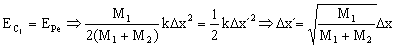
Y tenemos la amplitud del nuevo movimiento armónico simple. La frecuencia angular de este movimiento varía, ya que la masa del sistema ha variado. La nueva frecuencia es:

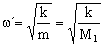
La ecuación del movimiento será entonces: