ν=4.46 s^-1

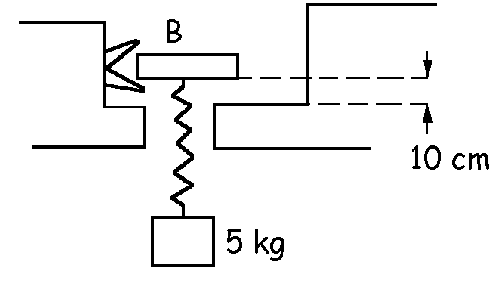
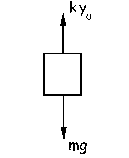Tomaremos a lo largo del problema el eje horizontal como eje X, y el eje vertical como eje Y. En primer lugar tenemos un la masa de 5 kg en equilibrio. Teniendo en cuenta la segunda ley de Newton:

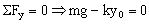
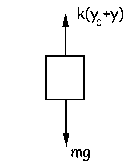Ahora supongamos que desplazamos el cuerpo anterior una cantidad «y» hacia abajo y lo dejamos oscilar. El cuerpo ya no está en equilibrio y para cualquier momento se debe verificar:

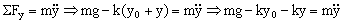
Sabemos por la ecuación de equilibrio que mg-ky₀=0 luego anulando este término nos queda:

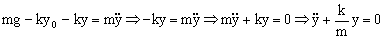
Es la ecuación de un movimiento armónico simple de frecuencia:

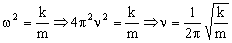
En esa ecuación desconocemos únicamente la constante del resorte k. Vamos a intentar determinarla.

Las fuerzas que actúan sobre el cuerpo en todo momento son las que aparecen reflejadas en el diagrama: mg (fuerza gravitatoria) y k(y_o+y) fuerza elástica del resorte. Ambas son conservativas, luego la energía mecánica del cuerpo permanece constante.

Vamos a considerar la energía mecánica del cuerpo en los instantes 1: reposo ⇒

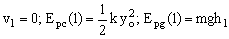
y en la posición 2: resorte estirado 5 cm estando momentáneamente en reposo:

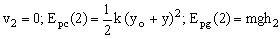
E_T1=E_T2 ⇒ ( E_Pg1-E_Pg2)+E_Pe1=E_Pe2

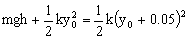
Sustituimos el alargamiento del equilibrio (y₀) por la expresión que hemos obtenido antes, y los datos conocidos por sus valores:

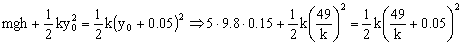
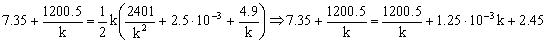
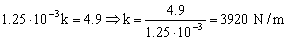
Una vez conocida la constante del resorte no hay más que sustituir en la ecuación que nos da la frecuencia de la oscilación:

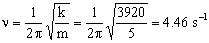
ν=4.46 s^-1