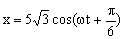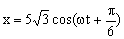
El movimiento resultante será la suma de esos dos movimientos armónicos, que tienen la misma frecuencia y la misma amplitud:
x=x1+x2
Además, el movimiento resultante también será armónico simple, luego tendrá la forma:
x=Asen(ωt+φ)
donde tendremos que determinar ω y φ. Sustituyendo cada movimiento por sus respectivas expresiones:
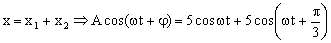
Desarrollaremos la expresión de la suma del coseno:
cos(a+b)=cosacosb-senasenb
Entonces:
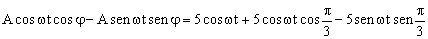
Igualamos por separado los términos que llevan el factor cosωt (proyecciones sobre el eje horizontal) y los términos que llevan el factor senωt (proyecciones sobre el eje vertical):
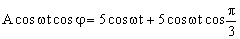
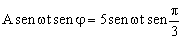
Simplificando:
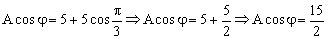
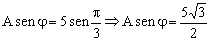
Dividiendo la segunda expresión entre la primera:
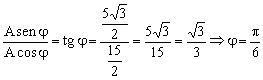
Y conocido el desfase podemos determinar la amplitud a partir de cualquiera de las ecuaciones en que aparece, por ejemplo:
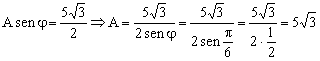
El movimiento resultante vale:
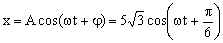
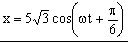
Gráficamente:
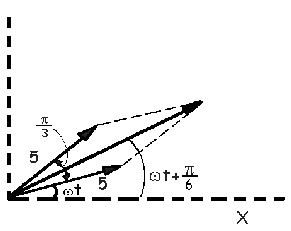
La longitud del fasor suma, que sería la amplitud del movimiento resultante, podemos determinarla, mediante el teorema del coseno
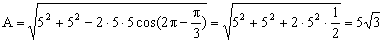
en cuanto a la fase como puede verse en la gráfica es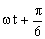 
, luego el movimiento resultante es: