x2+y2-xy-3=0
Analíticamente tendremos que los dos movimientos serán:
x=2cosωt
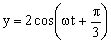
Aplicamos la expresión del coseno de una suma, que es:
cos(a+b)=cosacosb-senasenb
Y nos quedan las expresiones:
x=2cosωt
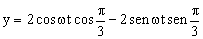
De la primera ecuación:
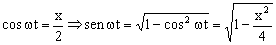
Sustituimos estos valores en la expresión de la y:
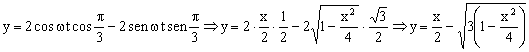
Aislamos la raíz para eliminarla:
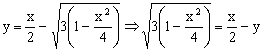
Elevando los dos miembros al cuadrado:

12-3x2=x2+4y2-4xy ⇒ 4x2+4y2-4xy-12=0 ⇒ x2+y2-xy-3=0
x2+y2-xy-3=0
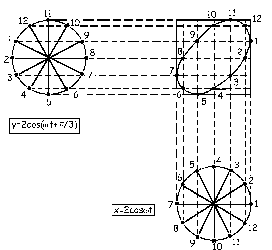 Ahora cada uno de los dos movimientos lo consideraremos como la proyección de un movimiento circular uniforme sobre un eje horizontal (movimiento x) o sobre un eje vertical (movimiento y). Como las velocidades angulares del móvil sobre las circunferencias generadoras son iguales, dividimos las dos circunferencias en 12 partes iguales. Además, adelantamos el primer punto de la circunferencia que representa el movimiento en y un ángulo de
Ahora cada uno de los dos movimientos lo consideraremos como la proyección de un movimiento circular uniforme sobre un eje horizontal (movimiento x) o sobre un eje vertical (movimiento y). Como las velocidades angulares del móvil sobre las circunferencias generadoras son iguales, dividimos las dos circunferencias en 12 partes iguales. Además, adelantamos el primer punto de la circunferencia que representa el movimiento en y un ángulo de 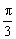 . Las intersecciones de las rectas paralelas a los ejes horizontal y vertical trazadas por los puntos hallados nos darán la curva buscada.
. Las intersecciones de las rectas paralelas a los ejes horizontal y vertical trazadas por los puntos hallados nos darán la curva buscada.
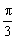 . Calcular gráfica y analíticamente la oscilación que resulta.
. Calcular gráfica y analíticamente la oscilación que resulta.